
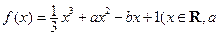 ,
,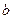 为实数)有极值,且在
为实数)有极值,且在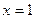 处的切线与直线
处的切线与直线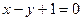 平行.
平行.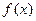 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;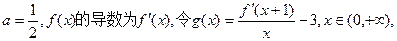
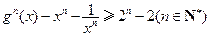 .
.
 的极小值为1
的极小值为1
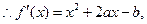 由题意
由题意
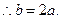 ① …………………………………………………………2分
① …………………………………………………………2分 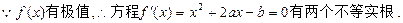
 ②
②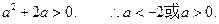
 …………………………………4分 (2)存在
…………………………………4分 (2)存在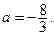 ………………………………………5分
………………………………………5分 ,
,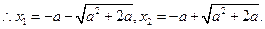
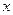 | 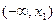 |  |  | 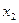 | 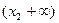 |
 | + | 0 | - | 0 | + |
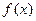 | 单调增 | 极大值 | 单调减 | 极小值 | 单调增 |
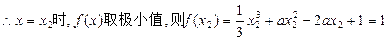 ,
,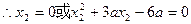 .……………………………………………………7分
.……………………………………………………7分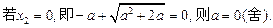 ……………………………………8分
……………………………………8分
 的极小值为1.………………………………9分
的极小值为1.………………………………9分 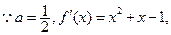
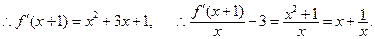
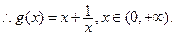 …………………………………………………10分
…………………………………………………10分 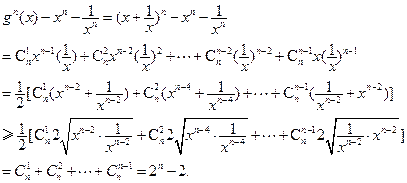
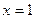 .……………………………………………………13分
.……………………………………………………13分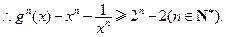 . ……………………………………………14分
. ……………………………………………14分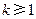 )时成立,即
)时成立,即
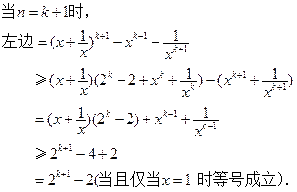
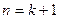 时原不等式成立.……………………………………………………13分
时原不等式成立.……………………………………………………13分 成立. …………………………………14分
成立. …………………………………14分

科目:高中数学 来源:不详 题型:解答题
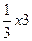 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。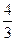 ,试确定b、c的值;
,试确定b、c的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com