练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题

    设θ∈[0，]，不等式sin2θ一(2＋a)sin(θ＋)＋2a＋3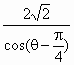＜恒成立，求实数a的取值范围．

    答案：
    解析：

    　　解：不等式可化为

    　　2sinθcosθ－(2＋a)(sinθ＋cosθ)＋2a＋3＜．

    　　令t＝sinθ＋cosθ＝sin(θ＋)．

    　　∵0≤θ≤，∴1≤t≤且2sinθcosθ＝t2－1．

    　　原不等式可化为(t2－1)－(2＋a)t＋2a＋3＜，

    　　即t2－(2＋a)t＋2a＜－2．变形为t(t－2)－a(t－2)＜．

    　　∵－1≤t－2≤－2，∴a＜＋t．

    　　要使上式恒成立，只需a＜(＋t)min即可．

    　　∵u＝t＋在[1，]上单调递减，

    　　∴(＋t)min＝2．

    　　故当a＜2时，对θ[0，]，原不等式恒成立．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：022

    设函数f(x)＝sin(ωx＋)(其中ω＞0，||＜)，给出五个论断：

    ①它的图象关于直线x＝对称；

    ②它的图象关于点(，0)对称；

    ③它的周期是π；

    ④它在区间[－，0]上是增函数；

    ⑤过点(0，)．

    以上其中两个论断作为条件，其余三个认断作为结论，写出你认为正确的一个命题，则该命题是________．

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：038

    设a＞0，解关于x的不等式＞0．

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    解答题

    设f(x)＝x2＋bx＋c(b，c为常数)，方程f(x)－x＝0的两个实根为x1，x2，且满足x1＞0，x2－x1＞1．

    (1)求证：b2＞2(b＋2c)；

    (2)设0＜t＜x1，比较f(t)与x1的大小；

    (3)当x∈[－1，1]时，对任意x都有|f(x)|≤1，

    求证：|1＋b|≤2．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设每台机床在1分钟内需要管理的概率为0.1，且这些机床是否需要工人去管理是彼此独立的．或一个工人负责4台机床，求1分钟内需要管理的机床的台数的平均台数．

    查看答案和解析>>

    同步练习册答案