Question

5．已知函数f（x）=$\frac{x-1}{a{e}^{x}}$-1（a∈R，a≠0）．
（1）当a=1时，求函数f（x）在（1，f（1））处的切线；
（2）若函数f（x）没有零点，求实数a的取值范围
（3）若函数f（x）恰有一个零点，试写出实数a的取值范围．

Answer 1

分析 （1）把a=1代入函数解析式，求出原函数的导函数，得到f′（1），再求出f（1），利用直线方程的点斜式得答案；
（2）利用导数分类求出函数的最值，由最大值大于0，最小值小于0求得实数a的取值范围；
（3）结合（2）画出函数图象的大致形状，由图象可得答案．

解答 解：（1）当a=1时，f（x）=$\frac{x-1}{{e}^{x}}-1$，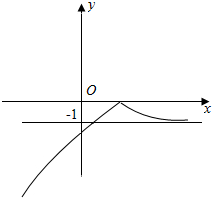
f′（x）=$\frac{{e}^{x}-（x-1）{e}^{x}}{{e}^{2x}}=\frac{2-x}{{e}^{x}}$，
∴f′（1）=$\frac{1}{e}$，又f（1）=-1，
∴函数f（x）在（1，f（1））处的切线为y+1=$\frac{1}{e}（x-1）$，
即x-ey-e-1=0；
（2）f（x）=$\frac{x-1}{a{e}^{x}}$-1，f′（x）=$\frac{a{e}^{x}-（x-1）a{e}^{x}}{{a}^{2}{e}^{2x}}=\frac{2-x}{a{e}^{x}}$，
若a＞0，则当x∈（-∞，2）时，f′（x）＞0，当x∈（2，+∞）时，f′（x）＜0，
∴$f（x）_{max}=f（2）=\frac{1}{a{e}^{2}}-1$，由$\frac{1}{a{e}^{2}}-1＜0$，得$a＞\frac{1}{{e}^{2}}$；
若a＜0，则当x∈（-∞，2）时，f′（x）＜0，当x∈（2，+∞）时，f′（x）＞0，
∴$f（x）_{min}=f（2）=\frac{1}{a{e}^{2}}-1$，由$\frac{1}{a{e}^{2}}-1＞0$，得a$＞\frac{1}{{e}^{2}}$，∴a∈∅．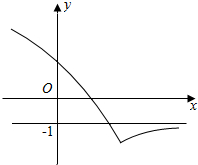
综上，若函数f（x）没有零点，则实数a的取值范围是（$\frac{1}{{e}^{2}}，+∞$）；
（3）由（2）知，当a＞0时，函数图象大致形状如上图，
只有$f（x）_{max}=\frac{1}{a{e}^{2}}-1=0$，即a=$\frac{1}{{e}^{2}}$时，函数f（x）恰有一个零点；
当a＜0时，函数图象大致形状如下图，
函数f（x）恰有一个零点．
综上，使函数f（x）恰有一个零点的实数a的范围是a＜0或a=$\frac{1}{{e}^{2}}$．

点评 本题考查利用导数研究过曲线上某点处的切线方程，训练了利用导数求函数的最值，考查函数零点的判定方法，体现了数形结合的解题思想方法，是中档题．