练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数的图象如图所示，则的单调递减区间为        ．

     



       

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知i为虚数单位，复数，i ，且，则实数的值为

     A．                 B．              C．或          D．或 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


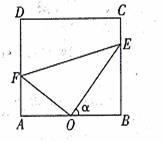
        学校生活区内建有一块矩形休闲区域ABCD，AB=100米，BC=50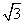米，为了便于同学们平时休闲散步，学校后勤部门将在这块区域内铺设三条小路OE、EF和OF，考虑到学校整体规划，要求O是AB的中点，点E在边BC上，点F在边AD上，且OE⊥OF,如图所示．

       （1）设∠BOE=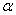，试将△OEF的周长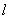表示成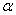的函数关系式，并求出此函数的定义域；

       （2）经核算，三条路每米铺设费用均为800元，试问如何设计才能使铺路的总费用最低？并求出最低总费用． 


    查看答案和解析>>

    科目：高中数学 来源： 题型：


        北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会，某公司为了竞标配套活动的相关代言，决定对旗下的某商品进行一次评估．该商品原来每件售价为25元，年销售8万件．

        ⑴据市场调查，若价格每提高1元，销售量将相应减少2000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？

        ⑵为了抓住申奥契机，扩大该商品的影响力，提高年销售量．公司决定立即对该商品进行全面技术革新和营销策略改革，并提高定价到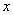元．公司拟投入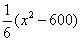万作为技改费用，投入50万元作为固定宣传费用，投入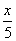万元作为浮动宣传费用．试问：当该商品改革后的销售量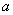至少应达到多少万件时，才可能使改革后的销售收入不低于原收入与总投入之和？并求出此时商品的每件定价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设为虚数单位，为正整数．

    ⑴证明：；

    ⑵结合等式“”证明：

    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知a>b>0，椭圆C1的方程为＋＝1，双曲线C2的方程为－＝1，C1与C2的离心率之积为，则C2的渐近线方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆C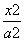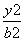：＋＝1(a＞b＞0)的离心率e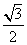＝，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2,左、右焦点分别为F1，F2．原点到直线A2B2的距离为．

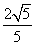    （1）求椭圆C的方程；

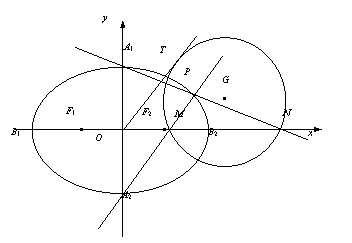    （2）P是椭圆上异于A1，A2的任一点,直线PA1，PA2，分别交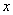轴于点N，M,若直线OT与过点M，N的圆G相切，切点为T.证明：线段OT的长为定值,并求出该定值.

                                                                        

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC的平面直观图△是边长为a的正三角形，则原△ABC的面积为（     ）

    A．        B．           C．         D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的定义域是（     ）

    A．  B． C．  D．，

    查看答案和解析>>

    同步练习册答案