Question

【题目】“绿水青山就是金山银山”。随着经济的发展，我国更加重视对生态环境的保护，2018年起，政府对环保不达标的养鸡场进行限期整改或勒令关闭。一段时间内，鸡蛋的价格起伏较大（不同周价格不同）。假设第一周、第二周鸡蛋的价格分别为元、元（单位：kg）；甲、乙两人的购买方式不同：甲每周购买3kg鸡蛋，乙每周购买10元钱鸡蛋.

（Ⅰ）若，求甲、乙两周购买鸡蛋的平均价格；

（Ⅱ）判断甲、乙两人谁的购买方式更实惠（平均价格低视为实惠），并说明理由.

Answer 1

【答案】（Ⅰ） ；（Ⅱ）见解析

【解析】

（Ⅰ）因此甲两周购买鸡蛋的平均价格为， 乙两周购买鸡蛋的平均价格为；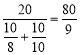

（Ⅱ）证法一：（比较法）：直接作差与0比较大小即可；

证法二（分析法）：依题意，且，

要证： 等价于证明，再转化为即可.

（Ⅰ）

甲两周购买鸡蛋的平均价格为， 乙两周购买鸡蛋的平均价格为，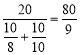

（Ⅱ）甲两周购买鸡蛋的平均价格为， 乙两周购买鸡蛋的平均价格为，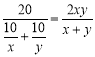

由（Ⅰ）知，时，乙两周购买鸡蛋的平均价格比甲两周购买鸡蛋的

平均价格低，猜测乙的购买方式更实惠。

证法一（比较法）：依题意，且，

，，

所以乙两周购买鸡蛋的平均价格比甲两周购买鸡蛋的平均价格低，

即乙的购买方式更实惠。

证法二（分析法）：依题意，且，

要证： ，

只需证：

只需证：

只需证：（已知）。

所以乙两周购买鸡蛋的平均价格比甲两周购买鸡蛋的平均价格低，

即乙的购买方式更实惠。