练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面直角坐标系xOy中，设定点A(a，a)，P是函数y＝ (x>0)图象上一动点．若点P，A之间的最短距离为2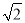，则满足条件的实数a的所有值为________．

     

    －1或

    【解析】本题考查函数的综合应用．设P(x0，)(x0>0)，|PA|＝＝，

    令x0＋＝t(t≥2)，

    令f(t)＝|PA|＝＝，

    对称轴t＝a，

    ①当a≤2时，f(t)在[2，＋∞)上为增函数，f(t)min＝f(2)＝＝2，

    即a2－2a－3＝0，∴a＝－1或a＝3(舍)，∴a＝－1.

    ②当a>2时，f(t)在[2，a]上为减函数，在[a，＋∞)上为增函数，f(t)min＝f(a)＝＝2，∴a＝.

    综上a的值为－1或.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：解答题

    某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元，已知甲、乙两户该月用水量分别为5x吨、3x吨．

    (1)求y关于x的函数；

    (2)若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量和水费．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-7函数的图象（解析版） 题型：选择题

    已知定义域在区间[0,2]上的函数y＝f(x)的图象如图所示，则y＝－f(2－x)的图象为 (　　)

     

     

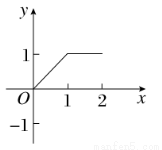
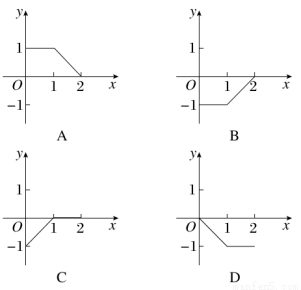
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    已知命题p：对?x∈R，?m∈R，使4x＋2xm＋1＝0.若命题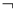p是假命题，则实数m的取值范围是(　　)

    A．[－2,2] B．[2，＋∞)

    C．(－∞，－2] D．[－2，＋∞)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    已知一元二次不等式f(x)<0的解集为{x|x<－1或x>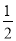}，则f(10x)>0的解集为(　　)

    A．{x|x<－1或x>－lg2} B．{x|－1<x<－lg2}

    C．{x|x>－lg2} D．{x|x<－lg2}

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：解答题

    已知f(x)＝x2＋ax＋3－a，若当x∈[－2,2]时，f(x)≥0恒成立，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题

    函数f(x)＝ax2＋ax－1在R上恒满足f(x)<0，则a的取值范围是(　　)

    A．a≤0 B．a<－4

    C．－4<a<0 D．－4<a≤0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：选择题

    已知函数f(x)为定义在R上的奇函数，当x≥0时，f(x)＝2x＋2x＋m(m为常数)，则f(－1)的值为(　　)

    A．－3 B．－1 C．1 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-12导数的应用二（解析版） 题型：选择题

    已知函数f(x)是定义在(－∞，0)∪(0，＋∞)上的偶函数，当x>0时，f(x)＝lnx－ax，若函数在定义域上有且仅有4个零点，则实数a的取值范围是(　　)

    A．(e，＋∞) B．(0，)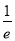

    C．(1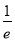，) D．(－∞，)

     

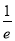    查看答案和解析>>

    同步练习册答案