练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝x2＋ax＋3－a，若当x∈[－2,2]时，f(x)≥0恒成立，求a的取值范围．

     

    －7≤a≤2.

    【解析】【解析】
    f(x)＝x2＋ax＋3－a＝(x＋)2－＋3－a.

    ①当－<－2，即a>4时，f(x)min＝f(－2)＝7－3a≥0，

    ∴a≤，又a>4，

    故此时a不存在．

    ②当－2≤－≤2，即－4≤a≤4时，f(x)min＝f(－)＝3－a－≥0，

    ∴a2＋4a－12≤0.

    ∴－6≤a≤2.

    又－4≤a≤4，∴－4≤a≤2.

    ③当－>2，即a<－4时，f(x)min＝f(2)＝7＋a≥0，

    ∴a≥－7.

    又a<－4，故－7≤a<－4.

    综上得－7≤a≤2.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：选择题

    某城市对一种售价为每件160元的商品征收附加税，税率为R%(即每销售100元征税R元)，若年销售量为(30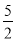－R)万件，要使附加税不少于128万元，则R的取值范围是(　　)

    A．[4,8] B．[6,10] C．[4%,8%] D．[6%,100%]

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：解答题

    是否存在实数a，使函数f(x)＝loga(ax2－x)在区间[2,4]上是增函数？如果存在，求出a的取值范围；如果不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    函数y＝2|x|的定义域为[a，b]，值域为[1,16]，当a变化时，函数b＝g(a)的图象可以是(　　)

     

     

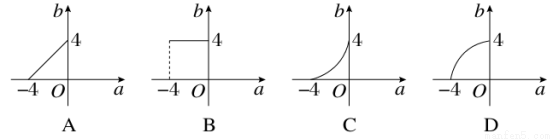
    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：填空题

    在平面直角坐标系xOy中，设定点A(a，a)，P是函数y＝ (x>0)图象上一动点．若点P，A之间的最短距离为2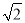，则满足条件的实数a的所有值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题

    设函数f(x)＝－2x2＋4x在区间[m，n]上的值域是[－6,2]，则m＋n的取值所组成的集合为(　　)

    A．[0,3] B．[0,4] C．[－1,3] D．[1,4]

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：选择题

    若f(x)是偶函数，且当x∈[0，＋∞)时，f(x)＝x－1，则f(x－1)<0的解集是(　　)

    A．(－1,0) B．(－∞，0)∪(1,2)

    C．(1,2) D．(0,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：解答题

    已知定义在区间(0，＋∞)上的函数f(x)满足f()＝f(x1)－f(x2)，且当x>1时，f(x)<0.

    (1)求f(1)的值；

    (2)判断f(x)的单调性；

    (3)若f(3)＝－1，解不等式f(|x|)<－2.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-12导数的应用二（解析版） 题型：选择题

    函数y＝x4－4x＋3在区间[－2,3]上的最小值为(　　)

    A．72 B．36 C．12 D．0

     

    查看答案和解析>>

    同步练习册答案