
 如图,在三棱柱ABC-A1B1C1中,侧棱CC1垂直于底面ABC,AC=3,AB=5,CB=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱CC1垂直于底面ABC,AC=3,AB=5,CB=4,AA1=4,点D是AB的中点.分析 (1)由勾股定理得AC⊥BC,由CC1⊥面ABC 得到CC1⊥AC,从而得到AC⊥面BCC1,故AC⊥BC1.
(2)C作CF⊥AB垂足为F,CF⊥面ABB1A1,面积法求CF,求出三角形DB1A1的面积,代入体积公式进行运算.
解答 (1)证明:在△ABC中,∵AC=3,AB=5,BC=4,
∴△ABC为直角三角形,∴AC⊥BC.
又∵CC1⊥平面ABC,∴CC1⊥AC,CC1∩BC=C,
∴AC⊥平面BCC1,∴AC⊥BC1.
(2)解:在△ABC中,过C作CF⊥AB,F为垂足,
∵平面ABB1A1⊥平面ABC,且平面ABB1A1∩平面ABC=AB,∴CF⊥平面ABB1A1,
由AC×BC=AB×h,得$h=\frac{3×4}{5}$=$\frac{12}{5}$.
∴三棱锥A1-B1CD的体积V=${V}_{C-{A}_{1}D{B}_{1}}$=$\frac{1}{3}{S}_{△{A}_{1}D{B}_{1}}h$=$\frac{1}{3}×\frac{1}{2}×5×4×\frac{12}{5}$=8.
点评 本题考查证明线线垂直、线面垂直的方法,求三棱锥的体积,求点C到面A1B1D的距离是解题的难点.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:解答题
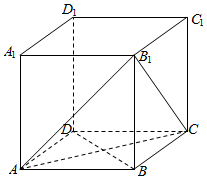 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
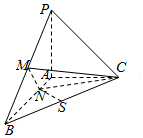 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
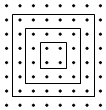 如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:
如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
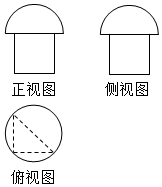 某几何体的三视图如图所示,其中正视图和侧视图均为全等的几何图形(下边是边长为2的正方形,上边为半圆),俯视图为等腰直角三角形(直角边的长为2)及其外接圆,则该几何体的体积是4+$\frac{4\sqrt{2}π}{3}$.
某几何体的三视图如图所示,其中正视图和侧视图均为全等的几何图形(下边是边长为2的正方形,上边为半圆),俯视图为等腰直角三角形(直角边的长为2)及其外接圆,则该几何体的体积是4+$\frac{4\sqrt{2}π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com