
分析 求出原函数的导函数,由导函数等于0,得到2a=x+$\frac{1}{x}$,利用基本不等式求得x+$\frac{1}{x}$的范围即可得到所求范围.
解答 解:由f(x)=$\frac{1}{2}$x2-2ax+lnx,
可得f'(x)=x-2a+$\frac{1}{x}$,
由题意可知存在实数x>0,使得f'(x)=x-2a+$\frac{1}{x}$=0,
即2a=x+$\frac{1}{x}$成立,
2a=x+$\frac{1}{x}$≥2(当且仅当x=$\frac{1}{x}$,即x=1时等号取到),
即a≥1,
即有实数a的取值范围是[1,+∞).
故答案为:[1,+∞).
点评 本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,同时考查转化思想的运用,是中档题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}π}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{{8\sqrt{2}π}}{3}$ | D. | $\frac{{\sqrt{3}π}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱CC1垂直于底面ABC,AC=3,AB=5,CB=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱CC1垂直于底面ABC,AC=3,AB=5,CB=4,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
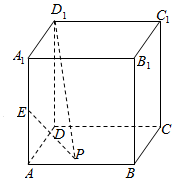 如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )
如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | M | 8 | 6 | 5 |
| A. | 6.4 | B. | 8 | C. | 9.6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 72种 | C. | 84种 | D. | 120种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com