
���� ��1������ԲM��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{3}}$=1�������㣨2$\sqrt{3}$��2$\sqrt{2}$����˫����N��$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0��������������ԲM�������ʻ�Ϊ�������г������飬���a��b���ɴ������˫����N�ķ��̣�
��2�������˫����N��$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1����ΪF��$-2\sqrt{2}$��0�����Ӷ������ߵ��߷���Ϊx=-2$\sqrt{2}$���ɴ�����������ߵķ��̣�
��� �⣺��1������ԲM��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{3}}$=1��
�����㣨2$\sqrt{3}$��2$\sqrt{2}$����˫����N��$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0��������������ԲM�������ʻ�Ϊ������
��$\left\{\begin{array}{l}{\frac{12}{{a}^{2}}-\frac{8}{{b}^{2}}=1}\\{\frac{\sqrt{{b}^{3}-4}}{\sqrt{{b}^{3}}}=\frac{a}{\sqrt{{a}^{2}+{b}^{2}}}}\end{array}\right.$��
���a=2��b=2��
��˫����N�ķ���Ϊ$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1��
��2��˫����N��$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1����ΪF��$-2\sqrt{2}$��0����
�������ߵ��߾���˫����N���㣬
�������ߵ��߷���Ϊx=-2$\sqrt{2}$��
�������ߵķ���Ϊy2=8$\sqrt{2}x$��
���� ���⿼��˫���߷��̺������߷��̵������е��⣬����ʱҪ�������⣬ע����Բ��˫���ߡ����������ʵĺ������ã�


 Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
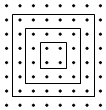 ��ͼ��ʾ��һϵ�������ν�����ָ����������չ����ģʽ���£�
��ͼ��ʾ��һϵ�������ν�����ָ����������չ����ģʽ���£��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
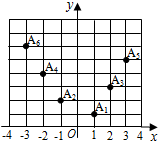 ��ͼ��ʾ������ֽ�ϵ�ÿ����Ԫ��ı߳�Ϊ1���������ϵ������㣺A1��x1��y1����A2��x2��y2��������A6��x6��y6���ĺᡢ������ֱ��Ӧ����{an}��n��N*����ǰ12�����������Ϊ�����������Ϊż����������ʾ��
��ͼ��ʾ������ֽ�ϵ�ÿ����Ԫ��ı߳�Ϊ1���������ϵ������㣺A1��x1��y1����A2��x2��y2��������A6��x6��y6���ĺᡢ������ֱ��Ӧ����{an}��n��N*����ǰ12�����������Ϊ�����������Ϊż����������ʾ��| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������S-ABCD�У�AB��AD��AB��CD��CD=3AB��ƽ��SAD��ƽ��ABCD��M���߶�AD��һ�㣬AM=AB��DM=DC��SM��AD��
��ͼ��������S-ABCD�У�AB��AD��AB��CD��CD=3AB��ƽ��SAD��ƽ��ABCD��M���߶�AD��һ�㣬AM=AB��DM=DC��SM��AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
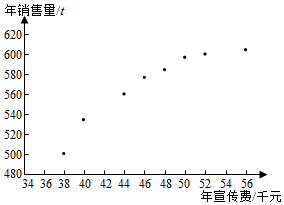 ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧԪ������������y����λ��t����������z����λ��ǧԪ����Ӱ�죮�Խ�8�����������xi����������yi��i=1��2������8���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ��
ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧԪ������������y����λ��t����������z����λ��ǧԪ����Ӱ�죮�Խ�8�����������xi����������yi��i=1��2������8���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ��| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^8{{{��{x_i}-\overline x��}^2}}$ | $\sum_{i=1}^8{{{��{w_i}-\overline w��}^2}}$ | $\sum_{i=1}^8{��{x_i}-\overline x����{y_i}-\overline y��}$ | $\sum_{i=1}^8{��{w_i}-\overline w����{y_i}-\overline y��}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1����2�������������� | B�� | ��1����2������������� | ||
| C�� | ��1�����������⣬��2����������� | D�� | ��1����������⣬��2������������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com