
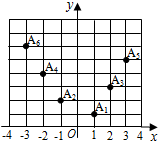
 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
分析 根据题目所给的六个点的坐标把十二个数字写出来,组成数列的前十二项,观察数列的特点,归纳出数列的通项公式,进而得到答案.
解答 解:若由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,
则a1=1,a2=1,a3=-1,a4=2,a5=2,a6=3,a7=-2,
a8=4,a9=3,a10=5,a11=-3,a12=6,
…
归纳可得:a4n-3=n,a4n-1=-n.
a2n=n,
∴a15=-4,
a2016=1008,
故答案为:-4,1008
点评 有的数列可以通过实际事件构造新数列,构造出一个我们较熟悉的数列,从而求出数列的通项公式.这类问题考查学生的灵活性,考查学生分析问题及运用知识解决问题的能力,这是一种化归能力的体现


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
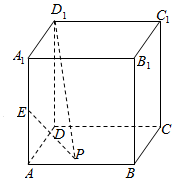 如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )
如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 72种 | C. | 84种 | D. | 120种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | c | 13 | 10 | -1 |
| y | 24 | 34 | 38 | d |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com