
分析 根据几何体的性质,转化为平面问题,利用勾股定理求解得出球的半径.
解答 解:∵AB=a,侧棱长为$\frac{{\sqrt{3}}}{2}a$,
∴O′A=$\frac{\sqrt{2}a}{2}$,O′A=O′B,
∴($\frac{\sqrt{3}a}{2}$)2=($\frac{\sqrt{2}a}{2}$)2+O′P2,O′P=$\frac{1}{2}a$,
∵设球的球心O,半径R,
∴R2=($\frac{\sqrt{2}a}{2}$)2+(R-$\frac{a}{2}$)2,
R=$\frac{\sqrt{3}a}{2}$,
∴球O的体积为:$\frac{4π×(\frac{\sqrt{3}a}{2})^{3}}{3}$=$\frac{\sqrt{3}{a}^{3}}{2}$
故答案为:$\frac{\sqrt{3}{a}^{3}}{2}$
点评 本题考查球O的体积,考查学生的计算能力,确定球的半径是关键,比较基础


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
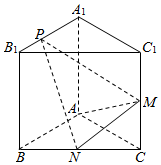 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
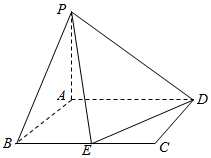 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
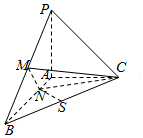 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
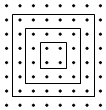 如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:
如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
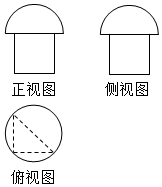 某几何体的三视图如图所示,其中正视图和侧视图均为全等的几何图形(下边是边长为2的正方形,上边为半圆),俯视图为等腰直角三角形(直角边的长为2)及其外接圆,则该几何体的体积是4+$\frac{4\sqrt{2}π}{3}$.
某几何体的三视图如图所示,其中正视图和侧视图均为全等的几何图形(下边是边长为2的正方形,上边为半圆),俯视图为等腰直角三角形(直角边的长为2)及其外接圆,则该几何体的体积是4+$\frac{4\sqrt{2}π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
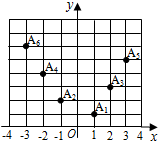 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com