
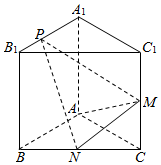
 ��ͼ����֪������ABC-A1B1C1�IJ�������洹ֱ��AA1=AB=AC=2��BC=2$\sqrt{2}$��M��N�ֱ���CC1��BC���е㣬��P��ֱ��A1B1�ϣ���$\overrightarrow{{A_1}P}=��\overrightarrow{{A_1}{B_1}}$��
��ͼ����֪������ABC-A1B1C1�IJ�������洹ֱ��AA1=AB=AC=2��BC=2$\sqrt{2}$��M��N�ֱ���CC1��BC���е㣬��P��ֱ��A1B1�ϣ���$\overrightarrow{{A_1}P}=��\overrightarrow{{A_1}{B_1}}$������ ��I�������ռ�ֱ������ϵ�����$\overrightarrow{AM}$��$\overrightarrow{PN}$�����ֻ꣬��֤��$\overrightarrow{AM}•\overrightarrow{PN}=0$���ɣ�
��II����Ȼƽ��ABC�ķ�����Ϊ$\overrightarrow{m}$=��0��0��1��������sin��=|cos��$\overrightarrow{PN}$��$\overrightarrow{m}$��|���sin�ȵ����ֵ������ͬ�����Ǻ����Ĺ�ϵ���tan�ȣ�
��� 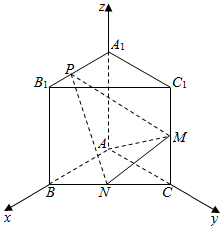 ֤������I����AB=AC=2��$BC=2\sqrt{2}$����AB2+AC2=BC2��
֤������I����AB=AC=2��$BC=2\sqrt{2}$����AB2+AC2=BC2��
��AB��AC����AB��AC��AA1�������ֱ��
��AΪԭ�㽨����ͼ��ʾ�Ŀռ�ֱ������ϵA-xyz��
��A1��0��0��2����B1��2��0��2����M��0��2��1����N��1��1��0����
��$\overrightarrow{{A_1}P}=��\overrightarrow{{A_1}{B_1}}$����P��2�ˣ�0��2������$\overrightarrow{PN}$=��1-2�ˣ�1��-2��.$\overrightarrow{AM}=��0��2��1��$��
��$\overrightarrow{AM}•\overrightarrow{PN}=��1-2�ˣ���0+1��2+��{-2}����1=0$��
�����ۦ�ȡ��ֵ��AM��PN��
����$\overrightarrow m$=��0��0��1����ƽ��ABC��һ����������
��$sin��=|{cos��\overrightarrow m��\overrightarrow{PN}��}|$=$\frac{|0+0-2|}{{\sqrt{{{��1-2�ˣ�}^2}+1+4}}}=\frac{2}{{\sqrt{{{��2��-1��}^2}+5}}}$��
�൱��=$\frac{1}{2}$ʱ����ȡ�����ֵ��
��ʱsin��=$\frac{{2\sqrt{5}}}{5}$��cos��=$\frac{{\sqrt{5}}}{5}$��tan��=2��
���� ���⿼���˿ռ�ǵļ��㣬�ռ��д�ֱ��ϵ���жϣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
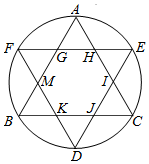 ��ͼ����ABC�͡�DEF����Բ�ڽ��������Σ���BC��EF����һ��֥��������ӵ���Բ�ڣ���A��ʾ�¼���֥�����ڡ�ABC�ڡ���B��ʾ�¼���֥�����ڡ�DEF�ڡ�����P��A��B�����ڣ�������
��ͼ����ABC�͡�DEF����Բ�ڽ��������Σ���BC��EF����һ��֥��������ӵ���Բ�ڣ���A��ʾ�¼���֥�����ڡ�ABC�ڡ���B��ʾ�¼���֥�����ڡ�DEF�ڡ�����P��A��B�����ڣ�������| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{3\sqrt{3}}{4��}$ | D�� | $\frac{\sqrt{3}}{2��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
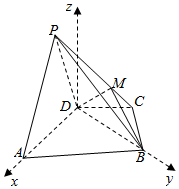 ��ͼ��������P-ABCD�У���������ABCD�У�AB��DC��ƽ��PAD��ƽ��ABCD����PAD�ǵȱ������Σ���֪BD=2AD=4��AB=2DC=2BC=2$\sqrt{5}$��$\overrightarrow{PM}$=m$\overrightarrow{MC}$����m��0��
��ͼ��������P-ABCD�У���������ABCD�У�AB��DC��ƽ��PAD��ƽ��ABCD����PAD�ǵȱ������Σ���֪BD=2AD=4��AB=2DC=2BC=2$\sqrt{5}$��$\overrightarrow{PM}$=m$\overrightarrow{MC}$����m��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ֱ������ABC-A1B1C1�У�AB=AA1��$��CAB=\frac{��}{2}$��
ֱ������ABC-A1B1C1�У�AB=AA1��$��CAB=\frac{��}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9��1 | B�� | 4��1 | C�� | 27��1 | D�� | 8��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}��}}{3}$ | B�� | $\frac{4��}{3}$ | C�� | $\frac{{8\sqrt{2}��}}{3}$ | D�� | $\frac{{\sqrt{3}��}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
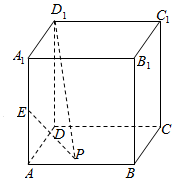 ��ͼ����������ABCD-A1B1C1D1�У�E�ǵ�AA1�е㣬PΪ����ABCD��һ���㣬��PD1��PE�����ABCD���ɵĽǷֱ�Ϊ��1����2����1����2����Ϊ0��������1=��2����P�Ĺ켣Ϊ�������ߵ�һ���֣�������
��ͼ����������ABCD-A1B1C1D1�У�E�ǵ�AA1�е㣬PΪ����ABCD��һ���㣬��PD1��PE�����ABCD���ɵĽǷֱ�Ϊ��1����2����1����2����Ϊ0��������1=��2����P�Ĺ켣Ϊ�������ߵ�һ���֣�������| A�� | ֱ�� | B�� | Բ | C�� | ��Բ | D�� | ������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com