
| A. | $\frac{{\sqrt{2}π}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{{8\sqrt{2}π}}{3}$ | D. | $\frac{{\sqrt{3}π}}{2}$ |
分析 当棱锥为球的内接四棱锥时,球体的体积最小,此时侧棱PC为球的直径.
解答 解: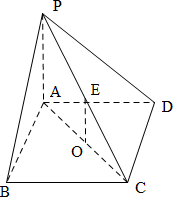 由题意可知当四棱锥的顶点都在球体毛坯的表面上时球体的体积最小.
由题意可知当四棱锥的顶点都在球体毛坯的表面上时球体的体积最小.
过球心E作平面ABCD的垂线EO,则O为底面ABCD的中心.
∵PA⊥平面ABCD,∴OE∥PA,
∵O为AC的中点,∴E为PC的中点,
∵PA=AB=BC=1,∴AC=$\sqrt{2}$,PC=$\sqrt{3}$.
∴球体的半径r=$\frac{1}{2}PC=\frac{\sqrt{3}}{2}$.
∴球体的体积V=$\frac{4}{3}π{r}^{3}=\frac{\sqrt{3}π}{2}$.
故选D.
点评 本题考查了棱锥与外接球的关系,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:解答题
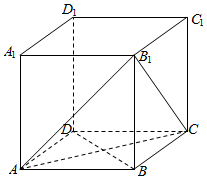 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
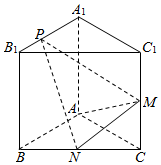 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
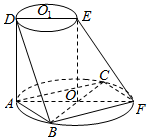 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
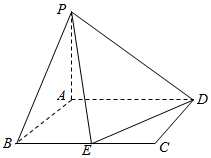 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
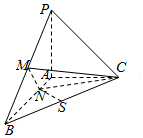 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
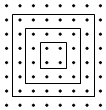 如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:
如图所示的一系列正方形将点阵分割,从内向外扩展,其模式如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com