
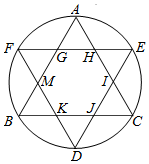
 如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )
如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{3}}{4π}$ | D. | $\frac{\sqrt{3}}{2π}$ |
分析 作出三条辅助线,根据已知条件这些小三角形全等,先求出P(B|A),再几何概型求出P(A),由此能求出P(A∩B)的值.
解答 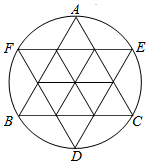 解:如图所示,作三条辅助线,根据已知条件这些小三角形全等,
解:如图所示,作三条辅助线,根据已知条件这些小三角形全等,
∴P(B|A)=$\frac{6}{9}$=$\frac{2}{3}$,
设△ABC的边长为2x,圆半径为r,则$\sqrt{(2x)^{2}-{x}^{2}}$×$\frac{2}{3}$=r,解得x=$\frac{\sqrt{3}}{2}r$,
∴S△ABC=$\frac{1}{2}×2x×\sqrt{3}x$=$\frac{\sqrt{3}}{2}r×\sqrt{3}×\frac{\sqrt{3}}{2}r$=$\frac{3\sqrt{3}{r}^{2}}{4}$,
${S}_{圆}=π{r}^{2}$,
∴P(A)=$\frac{{S}_{△ABC}}{{S}_{圆}}$=$\frac{\frac{3\sqrt{3}{r}^{2}}{4}}{π{r}^{2}}$=$\frac{3\sqrt{3}}{4π}$.
∴P(A∩B)=P(B|A)P(A)=$\frac{2}{3}×\frac{3\sqrt{3}}{4π}$=$\frac{\sqrt{3}}{2π}$.
故选:D.
点评 本题考查概率的计算,考查学生的计算能力,正确作出图形是解题的关键,解题时要注意几何概型计算公式的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 | |
| B. | 若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100 | |
| C. | 若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100 | |
| D. | 若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
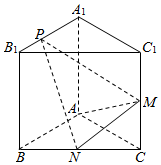 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,BC=2$\sqrt{2}$,M,N分别是CC1,BC的中点,点P在直线A1B1上,且$\overrightarrow{{A_1}P}=λ\overrightarrow{{A_1}{B_1}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com