
分析 先由概率公式求出一周内机器发生故障的次数ξ的概率,由题意知ξ=0,1,2,3次及以上分别对应的利润是5,2.5,0,-1万元,由求期望的公式求出即可.
解答 解:以ξ表示一周内机器发生故障的次数,则ξ~B(5,0.1),
∴P(ξ=k)=C5k×0.1k×0.95-k(k=0、1、…、5),
以η表示一周内获得的利润,则η=g(ξ),
而g(0)=5,g(1)=2.5,g(2)=0,g(ξ≥3)=-1
∴P(η=5)=P(ξ=0)=0.95=0.59045,
P(η=2.5)=P(ξ=1)=C51×0.11×0.94=0.32085,
P(η=0)=P(ξ=2)=C52×0.12×0.93=0.0729,
P(η=-1)=P(ξ≥3)=C53×0.13×0.92+C54×0.14×0.9+C55×0.15=0.00856,
∴Eη=5×0.59049+2.5×0.32805-0.0856=3.764015.
这台机器一周内可获利的均值是 37640.15元.
点评 本题考查离散型随机变量的期望与方差,求解的关键是计算出每一种利润所对应的概率,熟练掌握求期望的公式也很关键.


科目:高中数学 来源: 题型:选择题
| A. | x与y正相关,x与z负相关 | B. | x与y负相关,x与z正相关 | ||
| C. | z与y正相关,x与z正相关 | D. | x与y负相关,x与z负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
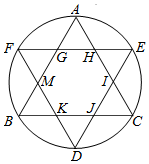 如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )
如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{3}}{4π}$ | D. | $\frac{\sqrt{3}}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com