
分析 根据题意,按甲乙的是否参加情况不同分情况讨论,分别由排列、组合公式计算其情况数目,进而由分类计数的加法公式,计算可得答案.
解答 解:根据题意安排甲和乙都参加,
则甲可以在心理辅导的工作中干一个活,甲若干医疗服务,则乙有3种结果,甲若不干医疗服务,则甲有2种选择,乙有2种选择.共有3+2×2=7种结果
另外两个活可以从三个人中选两个有A32=6种结果,共有7×6=42种结果,
甲和乙只有一个参加,另外三个人都参加,共有C21C31A33=36,
∴共有36+42=78种结果,
故答案为:78.
点评 本题考查排列、组合的综合运用,注意要根据题意,进而按一定顺序分情况讨论,对于有限制条件的元素要首先安排.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.3 | x | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
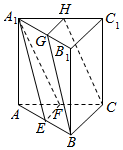 如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com