Question

7．设M，N分别为三棱锥P-ABC的棱AB，PC的中点，三棱锥P-ABC的体积记为V₁，三棱锥P-AMN的体积记为V₂，则$\frac{{V}_{2}}{{V}_{1}}$=$\frac{1}{4}$．

Answer 1

分析 由题意画出图形，利用N为棱PC的中点，且三棱锥P-ABC的体积记为V₁，得到${V}_{P-ABN}=\frac{1}{2}{V}_{1}$，再由M为棱AB的中点，得到${V}_{A-PMN}={V}_{B-PMN}=\frac{1}{4}{V}_{1}$，由等积法得到${V}_{P-AMN}=\frac{1}{4}{V}_{1}$，则$\frac{{V}_{2}}{{V}_{1}}$可求．

解答 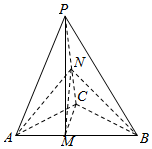解：如图，

∵N为棱PC的中点，且三棱锥P-ABC的体积记为V₁，
∴${V}_{P-ABN}=\frac{1}{2}{V}_{1}$，
又M为棱AB的中点，
则${V}_{A-PMN}={V}_{B-PMN}=\frac{1}{4}{V}_{1}$，
∴${V}_{P-AMN}=\frac{1}{4}{V}_{1}$，
即$\frac{{V}_{2}}{{V}_{1}}=\frac{1}{4}$．
故答案为：$\frac{1}{4}$．

点评 本题考查棱柱、棱锥及棱台的体积，训练了等积法的运用，是中档题．