
分析 设球的半径为1,则正方体棱长为2,根据正四棱锥与内切球的关系,列方程得出正四棱锥的底面边长和高的关系,代入棱锥的体积公式求出V1的最小值.
解答 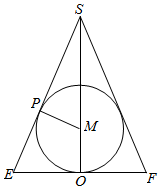 解:设球的半径r=1,则正方体的棱长为2r=2,∴V2=23=8
解:设球的半径r=1,则正方体的棱长为2r=2,∴V2=23=8
作正四棱锥过高SO和底面对边中点的截面SEF,则球的大圆为等腰三角形SEF的内切圆.
设正四棱锥的底面边长为a,高为h,则OE=PE=$\frac{a}{2}$,PM=MO=1,SM=h-1,SE=$\sqrt{{h}^{2}+\frac{{a}^{2}}{4}}$,
∴SP=$\sqrt{(h-1)^{2}-1}$=$\sqrt{{h}^{2}-2h}$.
∴$\sqrt{{h}^{2}-2h}$+$\frac{a}{2}$=$\sqrt{{h}^{2}+\frac{{a}^{2}}{4}}$,即h2-2h+$\frac{{a}^{2}}{4}$+a$\sqrt{{h}^{2}-2h}$=h2+$\frac{{a}^{2}}{4}$,
∴a=$\frac{2h}{\sqrt{{h}^{2}-2h}}$.
∴V1=$\frac{1}{3}$a2h=$\frac{4}{3}$•$\frac{{h}^{2}}{h-2}$=$\frac{4}{3}$•(h-2+$\frac{4}{h-2}$+4)≥$\frac{4}{3}×(2\sqrt{4}+4)$=$\frac{32}{3}$.
∴k=$\frac{{V}_{1}}{{V}_{2}}$=$\frac{{V}_{1}}{8}$≥$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了棱柱,棱锥与内切球的位置关系,棱锥的体积计算,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=0或3x-y-3=0 | B. | y=0或27x-4y-27=0 | ||
| C. | y=0或x=1 | D. | x=1或3x-y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 5.2 | 6.5 | 7.0 | 7.5 | 8.8 |
| A. | 10.8 | B. | 11.8 | C. | 12.8 | D. | 9.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
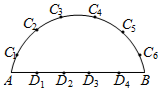 如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4,则:
如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4,则:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 4.5 | B. | 3.5 | C. | 3.15 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com