
| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
分析 根据$\overrightarrow{P{F_2}}$=2$\overrightarrow{{F_2}Q}$,且$\overrightarrow{{F_1}Q}$•$\overrightarrow{PQ}$=0,结合直角三角形的性质,建立三角形的边角关系,利用双曲线的定义得到关于a,c的方程进行求解即可.
解答 解:∵若$\overrightarrow{P{F_2}}$=2$\overrightarrow{{F_2}Q}$,
∴|$\overrightarrow{P{F_2}}$|=2|$\overrightarrow{{F_2}Q}$|,
∵$\overrightarrow{{F_1}Q}$•$\overrightarrow{PQ}$=0,∴$\overrightarrow{{F_1}Q}$⊥$\overrightarrow{PQ}$,
即∠F1QF2为直角,
则设|$\overrightarrow{P{F_2}}$|=2m,|$\overrightarrow{{F_2}Q}$|=m,
则|F1F2|=2c,
则|F1Q|=$\sqrt{4{c}^{2}-{m}^{2}}$,|F1P|=$\sqrt{4{c}^{2}-{m}^{2}+9{m}^{2}}$=$\sqrt{4{c}^{2}+8{m}^{2}}$,
则|F1Q|-|F2Q|=$\sqrt{4{c}^{2}-{m}^{2}}$-m=2a,①
|F1P|-|F2P|$\sqrt{4{c}^{2}+8{m}^{2}}$-2m=2a,②,
则$\sqrt{4{c}^{2}-{m}^{2}}$-m=$\sqrt{4{c}^{2}+8{m}^{2}}$-2m,
即$\sqrt{4{c}^{2}-{m}^{2}}$+m=$\sqrt{4{c}^{2}+8{m}^{2}}$,
平方整理得17m2=4c2,
则m2=$\frac{4{c}^{2}}{17}$,m=$\frac{2c}{\sqrt{17}}$,代回①得$\sqrt{4{c}^{2}-\frac{4{c}^{2}}{17}}$-$\frac{2c}{\sqrt{17}}$=2a,
即$\frac{8c}{\sqrt{17}}$-$\frac{2c}{\sqrt{17}}$=$\frac{6c}{\sqrt{17}}$=2a,
即离心率e=$\frac{c}{a}$=$\frac{{\sqrt{17}}}{3}$,
故选:B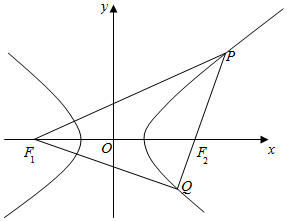
点评 本题主要考查双曲线离心率的计算,根据直角三角形的边角关系建立方程组,求出a,c的关系是解决本题的关键.综合性较强,运算量较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 |
| y | 6 | 4 | 5 |
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com