练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．有三对夫妻共6个人，站成一排照相，只有一对夫妻不相邻的站法共有（　　）
    A．72B．144C．48D．8

    分析 根据题意，分3步进行分析，把其中2对夫妻捆绑在一起，分别看做一个复合元素，再把这两个复合元素全排，形成了3个空，把另一对夫妻分别插入到其中两个空中，分别求出每一步的情况数目，由分步计数原理计算可得答案．

    解答 解：根据题意，分3步进行分析：
    ①、把其中2对夫妻捆绑在一起，分别看做一个复合元素，考虑其顺序，有A22A22种情况，
    ②、再把这两个复合元素全排，有A22种顺序，排好后形成了3个空，
    ③、把另一对夫妻分别插入到其中两个空中，有A32种情况，
    故有C32A22A22A22A32=144种不同的站法，
    故选：B．

    点评 本题考查了分步计数原理，相邻用捆绑，不相邻用插空，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．在平面直角坐标系xOy中，曲线y=xlnx在x=e处的切线与两坐标轴围成的三角形的面积是$\frac{e^2}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知双曲线C1：$\frac{x^2}{3}$-$\frac{{16{y^2}}}{p^2}$=1的左焦点在抛物线C2：y2=2px（p＞0）的准线上，则双曲线C1的离心率为（　　）
    A．$\frac{4}{3}$B．$\sqrt{3}$C．$\frac{{2\sqrt{3}}}{3}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上一点P，过双曲线中心的直线交双曲线于A，B两点，记直线PA，PB的斜率分别为k1，k2（k1，k2均不为零），当$\frac{4}{{{k_1}{k_2}}}$+ln|k1|+ln|k2|最小时，双曲线的离心率为（　　）
    A．$\sqrt{5}$B．2C．$\sqrt{2}+2$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．一个正四棱锥和一个正方体，它们有半径相同的内切球，记正四棱锥的体积为V1，正方体的体积为V2，且V1=kV2，则实数k的最小值为$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．用1，2，3，4这四个数能组成64个没有重复数字的整数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．两张卡片的正、反两面分别写有1，2；3，4，将这两张卡片排成一排，可以构成8个不同的两位数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

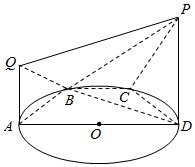    11．如图，等腰梯形ABCD的底角A等于60°，其外接圆圆心O在边AD上，直角梯形PDAQ垂直于圆O所在平面，∠QAD=∠PDA=90°，且AD=2AQ=4
    （1）证明：平面ABQ⊥平面PBD；
    （2）若二面角D-PB-C的平面角等于45°，求多面体PQABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=$\frac{x}{a}$+$\frac{a}{x}$（a为常数，x＞0），
    （Ⅰ）求函数f（x）在（0，+∞）上的单调区间；
    （Ⅱ）当a=$\frac{1}{2}$时
    （1）若曲线y=f（x）在点（x0，f（x0））处的切线与直线2x+3y-3=0垂直，求曲线在该点处的切线方程；
    （2）求证：f（x）＞lnx+$\frac{1}{2}x$．

    查看答案和解析>>

    同步练习册答案