
分析 首先分析题目求$\frac{x^3}{y^4}$的最大值的问题.不等式$\frac{x^3}{y^4}$的等价转换思想可得到$(\frac{{x}^{2}}{y})^{2}•\frac{1}{x{y}^{2}}$,然后求解各个表达式的范围,即可求解$\frac{x^3}{y^4}$的最大值.
解答 解:因为实数x,y满足3≤xy2≤8,4≤$\frac{x^2}{y}$≤9,
则有:($\frac{{x}^{2}}{y}$)2∈[16,81],$\frac{1}{x{y}^{2}}$∈[$\frac{1}{8}$,$\frac{1}{3}$],
再根据 $\frac{x^3}{y^4}$=$(\frac{{x}^{2}}{y})^{2}•\frac{1}{x{y}^{2}}$∈[2,27],即当且仅当x=3,y=1取得等号,
即$\frac{x^3}{y^4}$的最大值是27.
故答案为:27.
点评 本题主要考查不等式的基本性质和等价转化思想,等价转换思想在考试中应用不是很广泛,但是对于特殊题目能使解答更简便,也需要注意,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.3 | x | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,-2] | B. | (-5,-2) | C. | (2,5) | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
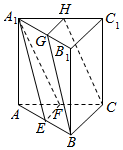 如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
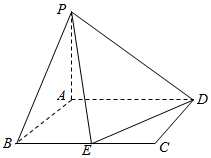 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com