
分析 由极坐标与直角坐标的关系:x=ρcosθ,y=ρsinθ,可得表示直线x=3;再将θ=$\frac{π}{6}$,$\frac{π}{4}$,$\frac{π}{3}$,-$\frac{π}{3}$,分别代入极坐标方程,由特殊角的三角函数值,即可得到所求极坐标.
解答 解:由极坐标与直角坐标的关系:x=ρcosθ,y=ρsinθ,
可得极坐标方程ρcosθ=3(ρ>0,-$\frac{π}{2}$<θ<$\frac{π}{2}$)表示直线x=3(y∈R);
当θ=$\frac{π}{6}$,由ρcos$\frac{π}{6}$=3,可得ρ=2$\sqrt{3}$,即极坐标为(2$\sqrt{3}$,$\frac{π}{6}$);
当θ=$\frac{π}{4}$,由ρcos$\frac{π}{4}$=3,可得ρ=3$\sqrt{2}$,即极坐标为(3$\sqrt{2}$,$\frac{π}{4}$);
当θ=$\frac{π}{3}$,由ρcos$\frac{π}{3}$=3,可得ρ=6,即极坐标为(6,$\frac{π}{3}$);
当θ=-$\frac{π}{3}$,由ρcos(-$\frac{π}{3}$)=3,可得ρ=6,即极坐标为(6,-$\frac{π}{3}$).
点评 本题考查极坐标和直角坐标的关系:x=ρcosθ,y=ρsinθ,考查特殊角的三角函数值,以及运算能力,属于基础题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
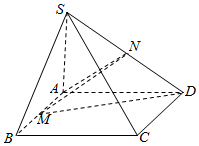 如图在四棱锥S-ABCD中,底面ABCD为正方形,顶点S在底面上的投影为A点,M,N分别是AB,SD的中点,且SB=5,AB=3.
如图在四棱锥S-ABCD中,底面ABCD为正方形,顶点S在底面上的投影为A点,M,N分别是AB,SD的中点,且SB=5,AB=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
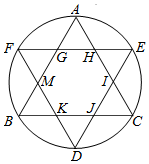 如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )
如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF,将一粒芝麻随机地扔到该圆内,用A表示事件“芝麻落在△ABC内”,B表示事件“芝麻落在△DEF内”,则P(A∩B)等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{3}}{4π}$ | D. | $\frac{\sqrt{3}}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
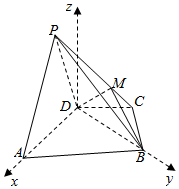 如图,在四棱锥P-ABCD中,底面梯形ABCD中,AB∥DC,平面PAD⊥平面ABCD,△PAD是等边三角形,已知BD=2AD=4,AB=2DC=2BC=2$\sqrt{5}$,$\overrightarrow{PM}$=m$\overrightarrow{MC}$,且m>0.
如图,在四棱锥P-ABCD中,底面梯形ABCD中,AB∥DC,平面PAD⊥平面ABCD,△PAD是等边三角形,已知BD=2AD=4,AB=2DC=2BC=2$\sqrt{5}$,$\overrightarrow{PM}$=m$\overrightarrow{MC}$,且m>0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com