
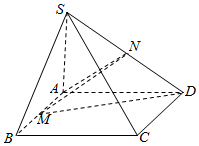
 如图在四棱锥S-ABCD中,底面ABCD为正方形,顶点S在底面上的投影为A点,M,N分别是AB,SD的中点,且SB=5,AB=3.
如图在四棱锥S-ABCD中,底面ABCD为正方形,顶点S在底面上的投影为A点,M,N分别是AB,SD的中点,且SB=5,AB=3.分析 (1)取SC的中点P,连结BP,PN.则可通过证明四边形BMNP是平行四边形得出MN∥BP,从而得出MN∥平面SBC;
(2)由SA⊥平面ABCD可得SA=4,于是N到平面ABCD的距离为SA的一半,于是VN-AMD=$\frac{1}{3}{S}_{△AMD}•\frac{1}{2}SA$.
解答 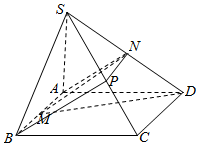 (1)证明:取SC的中点P,连结BP,PN.
(1)证明:取SC的中点P,连结BP,PN.
∵P,N分别是SC,SD的中点,
∴PN$\stackrel{∥}{=}$$\frac{1}{2}$CD,
∵四边形ABCD是矩形,M是AB的中点,
∴BM$\stackrel{∥}{=}$$\frac{1}{2}$CD.
∴BM$\stackrel{∥}{=}$PN,
∴四边形BMNP是平行四边形,
∴BP∥MN,∵BP?平面SBC,MN?平面SBC,
∴MN∥平面SBC.
(2)∵顶点S在底面上的投影为A点,
∴SA⊥平面ABCD,∴SA=$\sqrt{S{B}^{2}-A{B}^{2}}$=4.
∵N是SD的中点,∴N到平面ABCD的距离d=$\frac{1}{2}SA$=2.
∴VN-AMD=$\frac{1}{3}{S}_{△AMD}•d$=$\frac{1}{3}×\frac{1}{2}×3×\frac{3}{2}×2$=$\frac{3}{2}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | m | 5.6 | 6.1 | 7.4 | 9.3 |
| A. | 1.5 | B. | 1.55 | C. | 3.5 | D. | 1.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.3 | x | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:“?x∈R,x2-x-1>0,则命题p的否定为:“?x∈R,x2-x-1≤0” | |
| B. | “a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 | |
| C. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| D. | 直线a,b,为异面直线的充要条件是直线a,b不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com