
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 若命题p:“?x∈R,x2-x-1>0,则命题p的否定为:“?x∈R,x2-x-1≤0” | |
| B. | “a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件 | |
| C. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| D. | 直线a,b,为异面直线的充要条件是直线a,b不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 | |
| B. | 若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100 | |
| C. | 若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100 | |
| D. | 若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
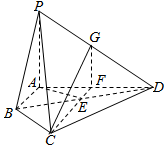 如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=$\frac{3}{2}$,连接CE并延长交AD于F.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=$\frac{3}{2}$,连接CE并延长交AD于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
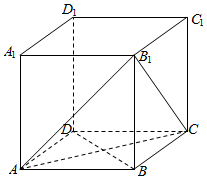 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
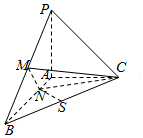 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=$\frac{1}{2}$AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.则SN与平面CMN所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com