
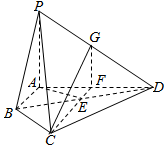
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=$\frac{3}{2}$,连接CE并延长交AD于F.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=$\frac{3}{2}$,连接CE并延长交AD于F.分析 (Ⅰ)利用直角三角形的判定得到∠BAD=$\frac{π}{2}$,且∠ABE=∠AEB=$\frac{π}{3}$.由△DAB≌△DCB得到△EAB≌△ECB,从而得到∠FED=∠FEA=$\frac{π}{3}$,所以EF⊥AD且AF=FD,结合题意得到FG是△PAD是的中位线,可得FG∥PA,根据PA⊥平面ABCD得FG⊥平面ABCD,得到FG⊥AD,最后根据线面垂直的判定定理证出AD⊥平面CFG;
(Ⅱ)利用等体积转换,求三棱锥VP-ACG的体积.
解答 (Ⅰ)证明:在△ABD中,∵E是BD的中点,
∴EA=EB=ED=AB=1,∴AE=$\frac{1}{2}$BD,
可得∠BAD=$\frac{π}{2}$,且∠ABE=∠AEB=$\frac{π}{3}$,
∵△DAB≌△DCB,
∴△EAB≌△ECB,
从而有∠FED=∠FEA=∠AEB=$\frac{π}{3}$,
故EF⊥AD,AF=FD,
又∵△PAD,中,PG=GD,
∴FG是△PAD的中位线,
∴FG∥PA.
又PA⊥平面ABCD,
∴FG⊥平面ABCD,
∵AD?平面ABCD,
∴GF⊥AD,
又∵EF,FG是平面CFG内的相交直线,
∴AD⊥平面CFG.
(Ⅱ)解:设BD与AC交于点O,
∵FG∥面PAC,
∴VP-ACG=VG-PAC=VF-PAC=$\frac{1}{3}$S△PACh
∵S△PAC=$\frac{1}{2}|PA||AC|$=$\frac{3\sqrt{3}}{4}$,h=$\frac{1}{2}|OD|$=$\frac{3}{4}$,
∴VP-ACG=$\frac{1}{3}×\frac{3\sqrt{3}}{4}×\frac{3}{4}$=$\frac{3\sqrt{3}}{16}$.
点评 本题在三棱锥中求证线面垂直,并求三棱锥VP-ACG的体积.着重考查了空间线面垂直的判定与性质,考查等体积转换等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
| 房屋大小 x/m2 | 80 | 105 | 110 | 115 | 135 |
| 销售价格y/万元 | 18.4 | 22 | 21.6 | 24.8 | 29.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
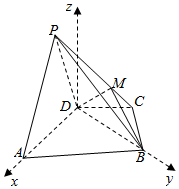 如图,在四棱锥P-ABCD中,底面梯形ABCD中,AB∥DC,平面PAD⊥平面ABCD,△PAD是等边三角形,已知BD=2AD=4,AB=2DC=2BC=2$\sqrt{5}$,$\overrightarrow{PM}$=m$\overrightarrow{MC}$,且m>0.
如图,在四棱锥P-ABCD中,底面梯形ABCD中,AB∥DC,平面PAD⊥平面ABCD,△PAD是等边三角形,已知BD=2AD=4,AB=2DC=2BC=2$\sqrt{5}$,$\overrightarrow{PM}$=m$\overrightarrow{MC}$,且m>0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 直三棱柱ABC-A1B1C1中,AB=AA1,$∠CAB=\frac{π}{2}$.
直三棱柱ABC-A1B1C1中,AB=AA1,$∠CAB=\frac{π}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com