
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
分析 用β表示α,代入条件式得出sin($β+\frac{π}{6}$),而cos(α+β)=cos(2β$+\frac{π}{3}$),使用二倍角公式即可求出答案.
解答 解:∵α-β=$\frac{π}{3}$,∴$α=β+\frac{π}{3}$,
∵cosα-cosβ=$\frac{1}{3}$,即cos($β+\frac{π}{3}$)-cosβ=$\frac{1}{3}$,
∴$\frac{1}{2}$cosβ+$\frac{\sqrt{3}}{2}$sinβ=-$\frac{1}{3}$,即sin($β+\frac{π}{6}$)=-$\frac{1}{3}$.
∴cos(α+β)=cos(α-β+2β)=cos(2β$+\frac{π}{3}$)=cos2($β+\frac{π}{6}$)=1-2sin2($β+\frac{π}{6}$)=1-2×(-$\frac{1}{3}$)2=$\frac{7}{9}$.
故选:C.
点评 本题考查了两角和差的余弦函数,二倍角公式,根据角的特点选择合适的三角公式是解决本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,-2] | B. | (-5,-2) | C. | (2,5) | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
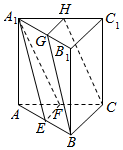 如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
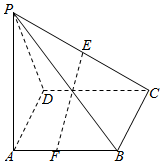 如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点
如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com