
分析 (1)利用捆绑法,即可得出结论;
(2)5名老师互不相邻,利用插空法;
(3)利用间接法,可得结论.
解答 解:(1)5名课代表必须排在一起,作为整体,与5门课的任课老师全排,有A66种方法,5名课代表之间,有A55种方法,∴5名课代表必须排在一起的排法有A66A55=86400种;
(2)5名老师互不相邻,利用插空法,5名课代表之间,有A55种方法,形成6个空,插入5名老师,有A65种方法,∴5名老师互不相邻的排法有A55A65=86400种;
(3)利用间接法,10个人全排,有A1010种方法,语文老师站在最左边,有A99种方法,数学老师站在最右边,有A99种方法,语文老师站在最左边且数学老师站在最右边,有A88种方法,∴语文老师不能站在最左边、数学老师不能站在最右边的排法有A1010-2A99+A88=73A88.
点评 本题考查排列知识的运用,考查学生的计算能力,正确计算是关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 地理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,-2] | B. | (-5,-2) | C. | (2,5) | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
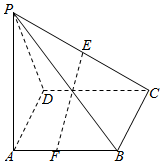 如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点
如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com