
分析 (1)求出原函数的导函数,得到函数在x=e处的导数,即在x=e处的切线的斜率,再求出切点坐标,代入直线方程点斜式得答案案;
(2)直接利用定积分求直线l与曲线C以及x轴所围成的面积.
解答 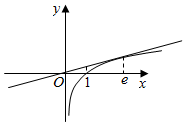 解:(1)由y=lnx,得$y′=\frac{1}{x}$,
解:(1)由y=lnx,得$y′=\frac{1}{x}$,
∴$y′{|}_{x=e}=\frac{1}{e}$,
又当x=e时,y=1,
∴曲线C:y=lnx在x=e处的切线方程为y-1=$\frac{1}{e}(x-e)$,
即x-ey=0;
(2)如图,直线l与曲线C以及x轴所围成的面积:
S=${∫}_{0}^{1}\frac{x}{e}dx{+∫}_{1}^{e}(\frac{x}{e}-lnx)dx$=$\frac{{x}^{2}}{2e}{|}_{0}^{1}+$$(\frac{{x}^{2}}{2e}-xlnx+x+C){|}_{1}^{e}$
=$\frac{1}{2e}+\frac{e}{2}-e+e+C-\frac{1}{2e}-1-C=\frac{e}{2}-1$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用定积分求曲边梯形的面积,是中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:填空题
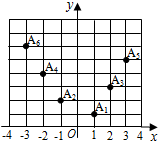 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:A1(x1,y1),A2(x2,y2),…,A6(x6,y6)的横、纵坐标分别对应数列{an}(n∈N*)的前12项,(即横坐标为奇数项,纵坐标为偶数项),如表所示:| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{3}{2}$,4) | C. | ($\frac{1}{4}$,$\frac{3}{2}$) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2)都是排列问题 | B. | (1)(2)都是组合问题 | ||
| C. | (1)是排列问题,(2)是组合问题 | D. | (1)是组合问题,(2)是排列问题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com