
分析 可以从三个圆心上找关系,构建矩形利用对角线相等即可求解出答案,利用圆的几何性质求解.
解答 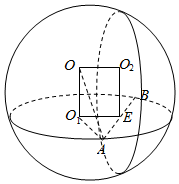 解:设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,
解:设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,
设圆O1的半径为O1A=$\sqrt{3}$,圆O2的半径为3于是O1E=O2E=$\sqrt{2}$
设圆O1的半径为$\sqrt{3}$,圆O2的半径为3,则$O{O_1}={O_2}E=2\sqrt{2}$,O2A=3,
所以球的半径$R=AO=\sqrt{O{O_1}^2+A{O_1}^2}=\sqrt{11}$,所求表面积为S=4πR2=44π.
故答案为:44π.
点评 本题主要考查球的有关概念以及两平面垂直的性质,是对基础知识的考查.解决本题的关键在于得到OO1EO2为矩形


科目:高中数学 来源: 题型:选择题
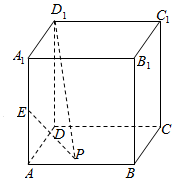 如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )
如图,在正方体ABCD-A1B1C1D1中,E是的AA1中点,P为地面ABCD内一动点,设PD1、PE与地面ABCD所成的角分别为θ1、θ2(θ1、θ2均不为0),若θ1=θ2,则动点P的轨迹为哪种曲线的一部分( )| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | c | 13 | 10 | -1 |
| y | 24 | 34 | 38 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
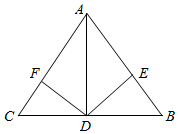 如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC
如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com