

分析 (Ⅰ)由勾股定理证明BM⊥AM,再利用平面ADM⊥平面ABCM,证明BM⊥平面ADM,从而可得AD⊥BM;
(Ⅱ)三棱锥M-ADE的体积就是三棱锥E-ADM的体积,而三角形ADM面积已知,则可以算出三棱锥E-ADM的高h,由(Ⅰ)可知BM⊥面ADM,通过h与BM的比值可确定E点在BD上的位置.
解答 (Ⅰ)证明:∵ABCD为长方形,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,
∴AM=2,BM=2,AB2=AM2+BM2,∴BM⊥AM,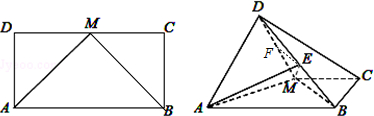
又∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM,
又∵AD?平面ADM,∴AD⊥BM;
(Ⅱ)解:在△BDM中,作EF∥BM交DM于F.
由(Ⅰ)知BM⊥平面ADM,
∴EF⊥平面ADM,EF是三棱锥E-MAD的高,
VM-ADE=VE-MAD=$\frac{1}{3}$($\frac{1}{2}$AD•DM)•EF=$\frac{1}{3}$,
∴$\frac{1}{6}×\sqrt{2}×\sqrt{2}$×EF=$\frac{1}{3}$,
则EF=1,
在△DMB中,BM=2,且EF∥BM,
∴EF为中位线,即E为BD的中点.
点评 本题考查空间中直线与直线的位置关系,考查利用等积法求三棱锥的体积,折叠问题重点分析折叠后未变的平行与垂直关系,线段的长,角度的不变的量;该题作为探究性问题,先把结论当成已知,然后结合已知条件列出方程求解,属中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{3}{2}$,4) | C. | ($\frac{1}{4}$,$\frac{3}{2}$) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2)都是排列问题 | B. | (1)(2)都是组合问题 | ||
| C. | (1)是排列问题,(2)是组合问题 | D. | (1)是组合问题,(2)是排列问题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号n | 1 | 2 | 3 | 4 | 5 | 6 |
| 成绩xn | 110 | 124 | 130 | x4 | 110 | 111 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com