
分析 当△ABC的面积取最大值时,OC与OA,OB的夹角相等,设∠AOC=∠BOC=α,则∠AOB=2π-2α,求出S的表达式,利用导数法求出最值,可得答案.
解答 解:当△ABC的面积取最大值时,OC与OA,OB的夹角相等;
设∠AOC=∠BOC=α,∠AOB=2π-2α,
∵OA=OB=2,OC=3$\sqrt{2}$,
∴△ABC的面积S=$\frac{1}{2}$OA•OB•sin(2π-2α)+$\frac{1}{2}$OA•OC•sinα+$\frac{1}{2}$OC•OB•sinα
=6$\sqrt{2}$sinα-2sin2α
则S′=6$\sqrt{2}$cosα-4cos2α=6$\sqrt{2}$cosα-8cos2α+4,
仅S′=0,则cosα=1(舍去),或cosα=-$\frac{\sqrt{2}}{4}$,
即当cosα=-$\frac{\sqrt{2}}{4}$时,S取最大值,此时sinα=$\frac{\sqrt{14}}{4}$,sin2α=$-\frac{\sqrt{7}}{4}$
即S的最大值为:$\frac{7\sqrt{7}}{2}$
故答案为:$\frac{7\sqrt{7}}{2}$
点评 本题考查的知识点是利用导数求函数的最值,三角形面积公式,转化困难,难度较大.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
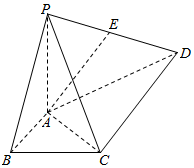 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=$\frac{π}{2}$,AB=BC=1,CD=2,PA⊥平面ABCD,E是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com