练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．某台小型晚会由6个节目组成，演出顺序有如下要求：节目甲、乙必须相邻且不能排在第一位，节目丙必须排在首尾，该台晚会节目演出顺序的编排方案共有（　　）
    A．60种B．72种C．84种D．120种

    分析 第一类，丙排在首位，把甲乙捆绑在一起和其3个节目全排，第二类，丙排在末位，先从除甲、乙、丙之外的3人选一个排在首位，把甲乙捆绑在一起和其2个节目全排，根据分类计数原理得到结果．

    解答 解：第一类，丙排在首位，把甲乙捆绑在一起和其3个节目全排，故有A22A44=48种，
    第二类，丙排在末位，先从除甲、乙、丙之外的3人选一个排在首位，把甲乙捆绑在一起和其2个节目全排，故有A31A22A33=36种，
    ∴故编排方案共有48+36=84种，
    故选C．

    点评 本题主要考查排列组合基础知识，考查分类与分步计数原理，分类加法计数原理：首先确定分类标准，其次满足：完成这件事的任何一种方法必属某一类，并且分别属于不同的两类的方法都是不同的方法，即“不重不漏”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

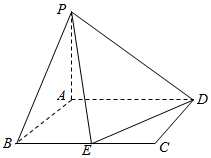    12．如图，PA⊥平面ABCD，矩形ABCD的边长AB=1，BC=2，E为BC的中点．
    （1）证明：PE⊥DE；
    （2）如果异面直线AE与PD所成角的大小为$\frac{π}{3}$，求PA的长及点A到平面PED的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

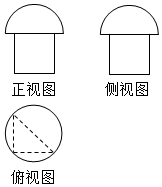    13．某几何体的三视图如图所示，其中正视图和侧视图均为全等的几何图形（下边是边长为2的正方形，上边为半圆），俯视图为等腰直角三角形（直角边的长为2）及其外接圆，则该几何体的体积是4+$\frac{4\sqrt{2}π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．将函数y=sinx+$\sqrt{3}$cosx的图象向右平移φ（φ＞0）个单位，再向上平移1个单位后，所得图象经过点（$\frac{π}{4}$，1），则φ的最小值为$\frac{7π}{12}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若函数f（x）=$\frac{1}{2}$x2-2ax+ln x存在垂直于y轴的切线，则实数a的取值范围是[1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=5|x|向右平移1个单位，得到y=g（x）的图象，则g（x）关于（　　）
    A．直线x=-1对称B．直线x=1对称C．原点对称D．y轴对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

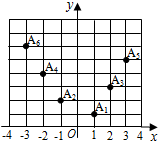    14．如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：A1（x1，y1），A2（x2，y2），…，A6（x6，y6）的横、纵坐标分别对应数列{an}（n∈N*）的前12项，（即横坐标为奇数项，纵坐标为偶数项），如表所示：
    a1a2a3a4a5a6a7a8a9a10a11a12
    x1y1x2y2x3y3x4y4x5y5x6y6
    按如此规律下去，则a15=-4，a2016=1008．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

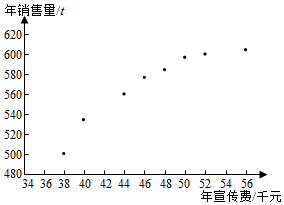    11．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．




    $\overrightarrow x$$\overrightarrow y$$\overrightarrow w$$\sum_{i=1}^8{{{（{x_i}-\overline x）}^2}}$$\sum_{i=1}^8{{{（{w_i}-\overline w）}^2}}$$\sum_{i=1}^8{（{x_i}-\overline x）（{y_i}-\overline y）}$$\sum_{i=1}^8{（{w_i}-\overline w）（{y_i}-\overline y）}$
    46.65636.8289.81.61469108.8
    表中wi=$\sqrt{x_i}$，$\overrightarrow w$=$\frac{1}{8}$$\sum_{i=1}^8{w_i}$
    （1）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
    （2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
    （3）已知这种产品的年利润z与x，y的关系为z=0.2y-x．根据（2）的结果，当年宣传费x=49时，年销售量及年利润的预报值是多少？
    附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：$\widehatβ=\frac{{\sum_{i=1}^n{（{u_i}-\overline u）（{v_i}-\overline{v）}}}}{{\sum_{i=1}^n{{{（{u_i}-\overline u）}^2}}}}$，$\widehatα=\overline v-\widehatβ\overline u$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若1＜a＜3，2＜b＜4，则$\frac{a}{b}$的范围是（　　）
    A．（$\frac{1}{2}$，1）B．（$\frac{3}{2}$，4）C．（$\frac{1}{4}$，$\frac{3}{2}$）D．（1，4）

    查看答案和解析>>

    同步练习册答案