
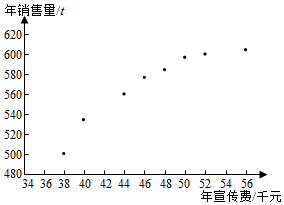
 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^8{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^8{({x_i}-\overline x)({y_i}-\overline y)}$ | $\sum_{i=1}^8{({w_i}-\overline w)({y_i}-\overline y)}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
分析 (1)由于散点图是否按直线型分布的判断;
(2)令w=$\sqrt{x}$,先求出y关于w线性的回归方程,再转化为y关于x的回归方程;
(3)把x=49代入回归方程求出销售量的预测值,再代入利润公式计算利润.
解答 解:(1)由散点图可以判断,y=c+d$\sqrt{x}$适宜作为年销售量y关于年宣传费x的回归方程类型.
(2)令w=$\sqrt{x}$,先建立y关于w的线性回归方程.
d=$\frac{\sum_{i=1}^{8}({ω}_{i}-\overline{ω})({y}_{i}-\overline{y})}{\sum_{i=1}^{8}({ω}_{i}-\overline{ω})^{2}}$=$\frac{108.8}{1.6}=68$,
c=$\overline{y}$-d$\overline{ω}$=563-68×6.8=100.6,
所以y关于w的线性回归方程为$\stackrel{∧}{y}$=100.6+68w,
因此y关于x的回归方程为$\stackrel{∧}{y}$=100.6+68$\sqrt{x}$.
(3)当x=49时,年销售量y的预报值$\stackrel{∧}{y}$=100.6+68$\sqrt{49}$=576.6,
年利润z的预报值z=576.6×0.2-49=66.32.
点评 本题考查了可化为线性相关的回归方程的求解以及利益回归方程进行数值预测,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 72种 | C. | 84种 | D. | 120种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 3.25 | B. | 2.6 | C. | 2.2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | c | 13 | 10 | -1 |
| y | 24 | 34 | 38 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
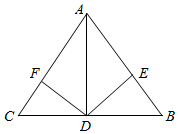 如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC
如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com