
【题目】直线l过点P(﹣2,1),
(1)若直线l与直线x+y﹣1=0平行,求直线l的方程;
(2)若点A(﹣1,﹣2)到直线l的距离为1,求直线l的方程.
【答案】
(1)解:由平行关系可设l的方程为:x+y+c=0
代入点P(﹣2,1)可得﹣2+1+c=0,解之可得c=1
故直线l的方程为:x+y+1=0
(2)解:若直线l的斜率不存在,则过P的直线为x=﹣2,到A的距离为1,满足题意,
若直线l的斜率存在,设为k,则l的方程为y﹣1=k(x+2)
化为一般式可得kx﹣y+2k+1=0,
由A到直线l的距离为1,可得 ![]() =1
=1
解之可得 ![]() ,所以直线方程为4x+3y+5=0
,所以直线方程为4x+3y+5=0
综上得所求的直线方程为x+2=0或4x+3y+5=0
【解析】(1)由平行关系可设l的方程为:x+y+c=0,代入点P(﹣2,1)可得c=1,可得直线的方程;(2)若直线l的斜率不存在,满足题意,若直线l的斜率存在,设为k,则l的方程为y﹣1=k(x+2),由点到直线的距离公式可得关于k的方程,解之可得.
【考点精析】通过灵活运用点到直线的距离公式,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: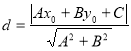 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表:
x |
|
| |||
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | ﹣2 |
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,画出该梯形的直观图A′B′C′D′,并写出其做法(要求保留作图过程的痕迹.)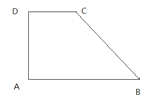
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:
| 1 | 2 | 3 | 4 |
| 12 | 28 | 42 | 56 |

(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:  ,
, ![]() ,
, ![]() .
.
参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正项数列
是正项数列![]() 的前
的前![]() 项和,且
项和,且![]() .
.
(Ⅰ)求数列![]() 通项公式;
通项公式;
(Ⅱ)是否存在等比数列![]() ,使
,使![]() 对一切正整数
对一切正整数![]() 都成立?并证明你的结论.
都成立?并证明你的结论.
(Ⅲ)设![]() (
(![]() ),且数列
),且数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com