
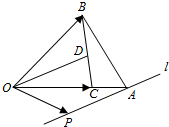
 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
分析 根据OD是△OBC的中线,得$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$.由直线l∥OD,可得存在实数k使$\overrightarrow{AP}$=k$\overrightarrow{OD}$,结合向量的基本定理以及向量的加法法则,进行运算即可算出则λ1-λ2的值.
解答  解:∵D是BC的中点,∴$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$
解:∵D是BC的中点,∴$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$
∵$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,∴$\overrightarrow{OA}$=$\frac{5}{4}$$\overrightarrow{OC}$,
∵直线l∥OD,∴存在实数k,使$\overrightarrow{AP}$=k$\overrightarrow{OD}$,
因此,$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}$=$\frac{5}{4}$$\overrightarrow{OC}$+k$\overrightarrow{OD}$=$\frac{5}{4}$$\overrightarrow{OC}$+k($\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$)=$\frac{k}{2}$$\overrightarrow{OB}$+($\frac{5}{4}$+$\frac{k}{2}$)$\overrightarrow{OC}$,
∵由已知,得$\overrightarrow{OP}={λ}_{1}\overrightarrow{OB}+{λ}_{2}\overrightarrow{OC}$
∴根据平面向量基本定理,得$\frac{k}{2}$=λ1且$\frac{5}{4}$+$\frac{k}{2}$=λ2
因此,λ1-λ2=$\frac{k}{2}$-($\frac{5}{4}$+$\frac{k}{2}$)=-$\frac{5}{4}$,
故选:D.
点评 本题在△OAB中,给出边的三等分点C和△OBC的中线OD,探索向量$\overrightarrow{OP}$表示成$\overrightarrow{OB}、\overrightarrow{OC}$的线性组合问题,着重考查了平面向量的线性运算、平面向量的基本定理及其意义等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
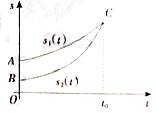 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )
甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲、v乙的关系是( )| A. | v甲>v乙 | B. | v甲<v乙 | C. | v甲=v乙 | D. | 大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
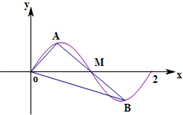 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)>0,f(b)<0 | D. | f(a)<0,f(b)>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com