
���� ��1��g��x��=��$\frac{1}{2}$��|x-a|=$\left\{\begin{array}{l}{��\frac{1}{2}��^{x-a}��x��a}\\{��\frac{1}{2}��^{a-x}��x��a}\end{array}\right.$���ڣ�-�ޣ�a���ϵ����������ڣ�a��+�ޣ��ϵ����ݼ������y=g��x����[1��$\frac{3}{2}$]�ϵ����ֵΪ$\frac{\sqrt{2}}{2}$���������ۣ��ɵ�����������ʵ��a��ֵ��
��2���֢�a��0����a��0������������ֱ�������������x1��[2��+��]���ܴ���Ψһ��x2�ʣ�-�ޣ�2����ʹ��p��x1��=p��x2��������ʵ��a��ȡֵ���ۺ����۽�����ɵô𰸣�
��� �⣺��1��g��x��=��$\frac{1}{2}$��|x-a|=$\left\{\begin{array}{l}{��\frac{1}{2}��^{x-a}��x��a}\\{��\frac{1}{2}��^{a-x}��x��a}\end{array}\right.$��
�ڣ�-�ޣ�a���ϵ����������ڣ�a��+�ޣ��ϵ����ݼ���
�ٵ�a��1ʱ����x=1ʱ��gmax��x��=$��\frac{1}{2}��^{1-a}$=$\frac{\sqrt{2}}{2}$����ã�a=$\frac{1}{2}$��
�ڵ�1��a��$\frac{3}{2}$ʱ����x=aʱ��gmax��x��=$��\frac{1}{2}��^{a-a}$=$\frac{\sqrt{2}}{2}$���⣻
�۵�a��$\frac{3}{2}$ʱ����x=$\frac{3}{2}$ʱ��gmax��x��=$��\frac{1}{2}��^{a-\frac{3}{2}}$=$\frac{\sqrt{2}}{2}$����ã�a=2��
����������a=2��$\frac{1}{2}$��
��2������a��0����x1��2��p��x1��=f��x1��=$\frac{a{x}_{1}}{4{x}_{1}^{2}+16}$��0��
x2��2��p��x2��=g��x2��=$��\frac{1}{2}��^{|{x}_{2}-a|}$��0��
��p��x1��=p��x2�������ܳ�����
����a��0����x��2ʱ��
p��x��=f��x��=$\frac{ax}{4{x}^{2}+16}$=$\frac{a}{4x+\frac{16}{x}}$��
��p��x����[2��+�ޣ��ϵ����ݼ���
��p��x1���ʣ�0��f��2��]=��0��$\frac{a}{16}$]��
1����a��2����x��2ʱ��p��x��=g��x��=��$\frac{1}{2}$��|x-a|=��$\frac{1}{2}$��-x+a=��$\frac{1}{2}$��a•2x��
��p��x���ڣ�-�ޣ�2���ϵ���������
�Ӷ�p��x2���ʣ�0����$\frac{1}{2}$��a-2����
Ҫʹp��x1��=p��x2��������
ֻ��$\frac{a}{16}$����$\frac{1}{2}$��a-2�������ɣ�
���ں���q��a��=$\frac{a}{16}$-��$\frac{1}{2}$��a-2��[2��+�ޣ��ϵ�����������q��4��=0��
��2��a��4��
2����0��a��2����x��2ʱ��p��x��=g��x��=��$\frac{1}{2}$��|x-a|=$\left\{\begin{array}{l}{��\frac{1}{2}��^{x-a}��x��a}\\{��\frac{1}{2}��^{a-x}��x��a}\end{array}\right.$��
��p��x���ڣ�-�ޣ�a���ϵ����������ڣ�a��2]�ϵ����ݼ���
�Ӷ�p��x2���ʣ�0��g��a��]=��0��1]��
Ҫʹp��x1��=p��x2��������
ֻ��$\frac{a}{16}$��1����$\frac{a}{16}$�ܣ�$\frac{1}{2}$��2-a�������ɣ�
��$\frac{a}{16}$�ܣ�$\frac{1}{2}$��2-a�������ɣ�
��0��a��2�ã�$\frac{a}{16}$��$\frac{1}{8}$����$\frac{1}{2}$��2-a��$\frac{1}{4}$��
�ʵ�0��a��2ʱ��$\frac{a}{16}$�ܣ�$\frac{1}{2}$��2-a�������
����������0��a��4��
���� ���⿼���֪ʶ���Ƿֶκ�����Ӧ�ã������ĵ����ԣ���������˼�룬�Ѷ��е���


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
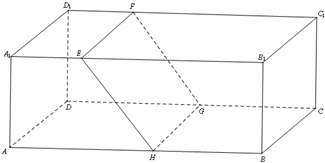 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�AB=16��AA1=8��BC=10����E��F �ֱ���A1B1C1D1�ϣ�A1E=D1F=4������E��F��ƽ�����˳���������ཻ������Χ��һ��������EFGH��
��ͼ���ڳ�����ABCD-A1B1C1D1�У�AB=16��AA1=8��BC=10����E��F �ֱ���A1B1C1D1�ϣ�A1E=D1F=4������E��F��ƽ�����˳���������ཻ������Χ��һ��������EFGH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
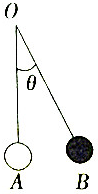 ��ͼ��ʾ��һ��������OAΪʼ�ߣ�OBΪ�ձߵĽǦȣ�-�У��ȣ��У���ʱ��t��s�����㺯����ϵʽ��=$\frac{1}{2}$sin��2t+$\frac{��}{2}$������t=0ʱ���ǦȵĴ�С������Ƶ���ǣ�������
��ͼ��ʾ��һ��������OAΪʼ�ߣ�OBΪ�ձߵĽǦȣ�-�У��ȣ��У���ʱ��t��s�����㺯����ϵʽ��=$\frac{1}{2}$sin��2t+$\frac{��}{2}$������t=0ʱ���ǦȵĴ�С������Ƶ���ǣ�������| A�� | $\frac{1}{2}$��$\frac{1}{��}$ | B�� | 2��$\frac{1}{��}$ | C�� | $\frac{1}{2}$���� | D�� | 2���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �м�Сֵ������ֵ | B�� | �м���ֵ����Сֵ | ||
| C�� | ���м�Сֵ��Ҳ�м���ֵ | D�� | ����Сֵ��Ҳ����ֵ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 9�� | C�� | 10�� | D�� | 7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\sqrt{3}$ | B�� | 0 | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com