
����Ŀ��ij���ڴ�����ȫ�����������������Ĺ����У�Ϊ�˵�������Դ�����ȫ�����������������������˽������������һ��֪ʶ�ʾ����飨һλ����ֻ�ܲμ�һ�Σ���ͨ������������õ��μ��ʾ������1000�˵ĵ÷֣�����100�֣�ͳ�ƽ�����±���ʾ��
��� |
|
|
|
|
|
|
|
Ƶ�� | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
��1�����аѵ÷ֲ�����80�ֵ������Ϊ������������������Ƶ�ʹ��Ƹ��ʣ��������������壬��Ӹ��е������������ȡһλ���鵽�������������ĸ��ʣ�
��2����Ƶ���ֲ������Դ�����Ϊ���˴��ʾ�����ĵ÷�![]() ������̬�ֲ�
������̬�ֲ�![]() ��
��![]() ����Ϊ��1000�˵÷ֵ�ƽ��ֵ��ͬһ�������ø�������������е�ֵ��ʾ����������̬�ֲ���֪ʶ��
����Ϊ��1000�˵÷ֵ�ƽ��ֵ��ͬһ�������ø�������������е�ֵ��ʾ����������̬�ֲ���֪ʶ��![]() ��
��
��3���ڣ�2���������£�����Ϊ�˴βμ��ʾ�����������ƶ����½���������
�������÷ֲ�����![]() �Ŀ��Ի���2��������ѣ��÷ֵ���
�Ŀ��Ի���2��������ѣ��÷ֵ���![]() �Ŀ��Ի���1��������ѣ�
�Ŀ��Ի���1��������ѣ�
������ÿ�λ����͵�������ѺͶ�Ӧ�ĸ���Ϊ��
���͵�������ѣ���Ԫ��Ԫ�� | 30 | 60 |
���� | 0.75 | 0.25 |
���������Ҫ�μӴ˴��ʾ����飬��![]() ����λ��Ԫ��Ϊ������μ��ʾ���������Ļ��ѣ���
����λ��Ԫ��Ϊ������μ��ʾ���������Ļ��ѣ���![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
�����ο������빫ʽ
![]() ����
����![]() �����
�����![]() ��
��
��![]() ����
����![]() ��
��
���𰸡���1��![]() ����2��
����2��![]() ����3���ֲ��м�������
����3���ֲ��м�������![]()
��������
��1���ɹŵ�����ʹ�ʽֱ�Ӽ���õ������
��2������Ƶ���ֲ����ɼ���õ�![]() ���ɴ�ȷ��
���ɴ�ȷ��![]() ��������̬�ֲ����ߵ����ʿ���ý����
��������̬�ֲ����ߵ����ʿ���ý����
��3������ȷ��![]() ���п��ܵ�ȡֵ�����ݶ����¼����ʹ�ʽ�����ÿ��ȡֵ��Ӧ�ĸ��ʣ��ɴ˵õ��ֲ��У�������ѧ�������㹫ʽ�������ѧ����.
���п��ܵ�ȡֵ�����ݶ����¼����ʹ�ʽ�����ÿ��ȡֵ��Ӧ�ĸ��ʣ��ɴ˵õ��ֲ��У�������ѧ�������㹫ʽ�������ѧ����.
��1����Ӹ��е������������ȡһλ���鵽������������Ϊ�¼�![]() ��
��
��![]() ��
��
��2��![]()
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��3��������֪��![]() ��
��![]() ��
��
![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
�� ��
��
![]() ��
��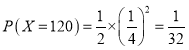 ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
![]() .
.


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӹ���������������ÿ����10��������ڳ���֮ǰ��Ҫ��ÿ�����������飬�˹����鷽�����£��ȴ�ÿ�������������ȡ4�����������ȡ�����������Ʒ���Ǵ�Ʒ����ֹͣ���飻����ȡ�����������1��������3����Ʒ�����ʣ�µ�6�������һ����.��֪ÿ���������ϸ�ĸ���Ϊ0.8��ÿ������Ƿ����ϸ����������ÿ��������˹������Ϊ2Ԫ.
��1����1������˹������ܷ���Ϊ![]() Ԫ����
Ԫ����![]() �ķֲ��У�
�ķֲ��У�
��2�������˹����鷽����л������鷽��������������Ҫ��ÿ���ÿ����������飬ÿ������ļ����Ϊ1.6Ԫ.����1000�������Ҫ���飬�Լ����ܷ��õ���ѧ����Ϊ���ݣ����˹���������������У�Ӧ��ѡ����һ����˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ�������ݷ��ٷ�չ��ʱ�������ڴ������˲ŵ�����ҲԽ��Խ�����λ���¿ɷ�Ϊ���ࣺ���ݿ��������ݷ����������ھ����ݲ�Ʒ.ij��2019���⼸�����λ��н�ʣ���λ����Ԫ/�£�������±���ʾ��
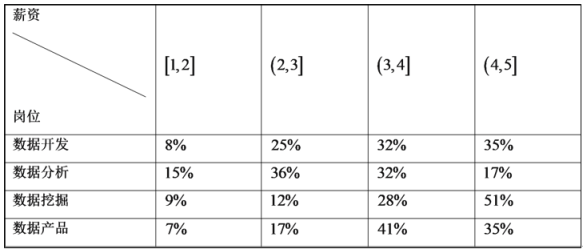
�ɱ������ݿɵø��и����λ��н��ˮƽ�ߵ����Ϊ�� ��
A.�����ھ����ݿ��������ݲ�Ʒ�����ݷ���
B.�����ھ����ݲ�Ʒ�����ݿ��������ݷ���
C.�����ھ����ݿ��������ݷ��������ݲ�Ʒ
D.�����ھ����ݲ�Ʒ�����ݷ��������ݿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ����������䣻
�ĵ����������䣻
��2����![]() ���ڽ�
���ڽ�![]() �Ķ�Ӧ�߷ֱ�Ϊ
�Ķ�Ӧ�߷ֱ�Ϊ![]() ����
����![]() ��������
��������![]() ������
������![]() ���ߣ���
���ߣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ������
������![]() .
.
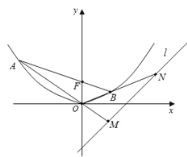
��1����������![]() �ķ��̣�
�ķ��̣�
��2����![]() ��ֱ�߽���������
��ֱ�߽���������![]() ��
��![]() ����.��ֱ��
����.��ֱ��![]() ��
��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�����ABB1A1�����Σ���CA��CB1��
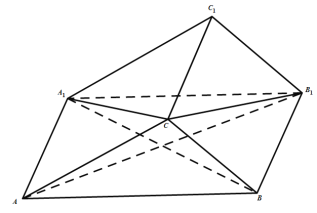
��1��֤������CBA1����CB1A��
��2������BAA1��60�㣬A1C��BC��BA1��������C��A1B1��C1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��BCD�У���ABD����CBD��Ϊ�߳�Ϊ2�ĵȱ������Σ��Ҷ����![]() ��ƽ���Ϊ120������������������ı����Ϊ��������
��ƽ���Ϊ120������������������ı����Ϊ��������
A.7��B.8��C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��PAC��ƽ��ABC��![]() ����ACΪб�ߵĵ���ֱ�������Σ�E��F��O�ֱ�ΪPA��PB��AC���е㣬
����ACΪб�ߵĵ���ֱ�������Σ�E��F��O�ֱ�ΪPA��PB��AC���е㣬![]() .
.

��1����G��OC���е㣬֤����![]() ��ƽ��
��ƽ��![]() ��
��
��2��֤������![]() �ڴ���һ��M��ʹFM��ƽ��BOE�����M��OA��OB�ľ���.
�ڴ���һ��M��ʹFM��ƽ��BOE�����M��OA��OB�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ����
����![]() ��ǰ
��ǰ![]() ��ͣ�������
��ͣ�������![]() ������
������![]() ��
��![]() ��������
��������
��1����![]() ʱ����
ʱ����![]() ��
��
��2����![]() ʱ��
ʱ��
��������֤������![]() �ǵȲ����У�
�ǵȲ����У�
��������������![]() ���ش���
���ش���![]() ʹ��
ʹ��![]() ����֪
����֪![]() ����
����![]() ��������
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com