
【题目】在四棱锥P﹣ABCD中, ![]() ,
, ![]() ,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O. 
(1)求证:O是AD中点;
(2)证明:BC⊥PB;
(3)求二面角A﹣PB﹣C的余弦值.
【答案】
(1)证明:∵△PAB和△PBD都是等边三角形,
∴PA=PB=PD,
又∵PO⊥底面ABCD,
∴OA=OB=OD,
则点O为△ABD的外心,又因为△ABD是直角三角形,
∴点O为AD中点
(2)证明:由(1)知,点P在底面的射影为点O,点O为AD中点,
于是PO⊥面ABCD,
∴BC⊥PO,
∵在Rt△ABD中,BD=BA,OB⊥AD,
∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
,
从而 ![]() 即CB⊥BO,
即CB⊥BO,
由BC⊥PO,CB⊥BO得CB⊥面PBO,
∴BC⊥PB
(3)解:以点O为原点,以OB,OD,OP所在射线为x轴,y轴,z轴建系如图,
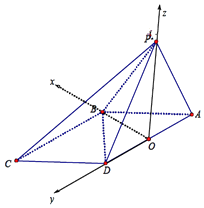
∵AB=2,则O(0,0,0), ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设面PAB的法向量为 ![]() ,则
,则 ![]() ,
, ![]() ,得
,得 ![]() ,
, ![]() ,
,
取x=1,得y=﹣1,z=1,
故 ![]() .
.
设面PBC的法向量为 ![]() ,则
,则 ![]() ,
, ![]() ,得s=0,
,得s=0, ![]() ,
,
取r=1,则t=1,故 ![]() ,
,
于是 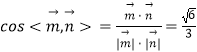 ,
,
由图观察知A﹣PB﹣C为钝二面角,
所以该二面角的余弦值为- ![]()
【解析】(1)证明PO⊥底面ABCD,说明点O为△ABD的外心,然后判断点O为AD中点.(2)证明PO⊥面ABCD,推出BC⊥PO,证明CB⊥BO,BC⊥PO,证明CB⊥面PBO,推出BC⊥PB.(3)以点O为原点,以OB,OD,OP所在射线为x轴,y轴,z轴建系,求出相关点的坐标,平面PAB的法向量,平面PBC的法向量,利用空间向量的数量积求解所以该二面角的余弦值即可.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC. (Ⅰ)求角B的大小;
(Ⅱ)若a=2,c=3,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为(x﹣3)2+y2=1,圆M的方程为(x﹣3﹣3cosθ)2+(y﹣3sinθ)2=1(θ∈R),过M上任意一点P作圆C的两条切线PA,PB,切点分别为A、B,则∠APB的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2x+alnx(a∈R).
(1)讨论函数f(x)的单调性;
(2)当t≥1时,不等式f(2t﹣1)≥2f(t)﹣3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,数列{bn}是等比数列,且b1=a1=1,b2=a3 , b3=a9
(1)求数列{an}的通项公式;
(2)求数列{anbn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com