
【题目】设集合![]() 为函数
为函数![]() 的定义域,集合
的定义域,集合![]() 为不等式
为不等式![]() 的解集.
的解集.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:
(1)利用题意首先求得集合A,B,然后求解交集可得A∩B= [1,2)
(2)首先求得![]() ,然后结合子集的定义得到关于实数a的不等式,求解不等式可得实数
,然后结合子集的定义得到关于实数a的不等式,求解不等式可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)由函数有意义得![]() ,即(1+x)(2-x)>0,
,即(1+x)(2-x)>0,
解得-1<x<2,即A={x|-1<x<2}.
解不等式(x-1)(x+2)≥0得x≤-2或x≥1,即B={x|x≤-2或x≥1}.
∴A∩B={x|1≤x<2}=[1,2).
(2)由(1)知RA={x|x≤-1或x≥2},
解不等式(ax-1)(x+2)≥0得x≤-2或x≥![]() ,即B={x|x≤-2或x≥
,即B={x|x≤-2或x≥![]() },
},
∵BRA,∴![]() ≥2,解得0<a≤
≥2,解得0<a≤![]() .
.
即实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学有学生 ![]() 人,其中一年级
人,其中一年级 ![]() 人,二、三年级各
人,二、三年级各 ![]() 人,现要用抽样方法抽取
人,现要用抽样方法抽取 ![]() 人形成样本,将学生按一、二、三年级依次统一编号为
人形成样本,将学生按一、二、三年级依次统一编号为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如果抽得号码有下列四种情况:
,如果抽得号码有下列四种情况:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
其中可能是由分层抽样得到,而不可能是由系统抽样得到的一组号码为 ![]()
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的奇数项是公差为
的奇数项是公差为![]() 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为![]() 的等差数列,
的等差数列, ![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和, ![]()
(1)若![]() ,求
,求![]() ;
;
(2)已知![]() ,且对任意的
,且对任意的![]() ,有
,有![]() 恒成立,求证:数列
恒成立,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() ,求当
,求当![]() 最大时,数列
最大时,数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() 的检测数据,结果统计如下:
的检测数据,结果统计如下:
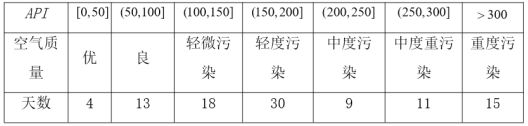
记某企业每天由空气污染造成的经济损失![]() (单位:元),空气质量指数
(单位:元),空气质量指数![]() 为
为![]() .在区间
.在区间![]() 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当![]() 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当![]() 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面![]() 列联表,并判断
列联表,并判断
能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)和g(x)满足:①在区间[a,b]上均有定义;②函数y=f(x)-g(x)在区间[a,b]上至少有一个零点,则称f(x)和g(x)在[a,b]上具有关系G.
(1)若f(x)=lgx,g(x)=3-x,试判断f(x)和g(x)在[1,4]上是否具有关系G,并说明理由;
(2)若f(x)=2|x-2|+1和g(x)=mx2在[1,4]上具有关系G,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(I)若![]() ,求函数
,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(II)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(III)令![]() ,
,![]() (
(![]() 是自然对数的底数),求当实数
是自然对数的底数),求当实数![]() 等于多少时,可以使函数
等于多少时,可以使函数![]() 取得最小值为3.
取得最小值为3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com