
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)由![]() ,得
,得![]() ,根据
,根据![]() 是函数
是函数![]() 的极值点,即可求解实数
的极值点,即可求解实数![]() 的值;(II)由
的值;(II)由![]() 在区间
在区间![]() 上单调递增,得
上单调递增,得![]() 在区间
在区间![]() 上恒成立,得到
上恒成立,得到![]() 对区间
对区间![]() 恒成立,设
恒成立,设![]() ,利用导数求解函数
,利用导数求解函数![]() 的最小值,即可求解实数
的最小值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由![]() ,得
,得![]() ,………………2分
,………………2分
∵![]() 是函数
是函数![]() 的极值点,
的极值点,
∴ ![]() ,解得
,解得![]() ,………4分
,………4分
经检验![]() 为函数,
为函数,![]() 的极值点,(不检验1分扣去)
的极值点,(不检验1分扣去)
所以![]() .……………5分
.……………5分
(Ⅱ)∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() 对区间
对区间![]() 恒成立,………8分
恒成立,………8分
令![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,有
,有![]() ……………12分
……………12分
∴![]() 的取值范围为
的取值范围为![]() …………13分
…………13分
法二:上同,
∴![]() 对区间
对区间![]() 恒成立,………………8分
恒成立,………………8分
令![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,在
,在![]() 上单调递增函数
上单调递增函数
∴![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ………………13分
………………13分
法三:∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() 在区间
在区间![]() 上恒成立,………………8分
上恒成立,………………8分
记![]() ,则
,则
![]() 或
或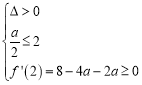
即![]() 或
或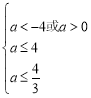
解得![]() ………………12分
………………12分
∴![]() 的取值范围为
的取值范围为![]() ……………13分
……………13分


科目:高中数学 来源: 题型:
【题目】已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() ,且
,且![]() 在区间
在区间![]() 上的最大值是12.
上的最大值是12.
(1)求![]() 的解析式;
的解析式;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图.
的信息如下图.

(1)求![]() ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,下顶点为
,下顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() (
(![]() 为坐标原点),如图,若抛物线
为坐标原点),如图,若抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且经过
,且经过![]() 点.
点.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于点
于点![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
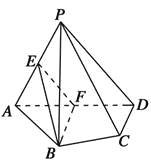
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com