Question

17．在区间（0，1）中随机地取出两个数，则两数之和大于$\frac{5}{6}$的概率是$\frac{47}{72}$．

Answer 1

分析 本题考查的知识点是几何概型的意义，关键是要找出（　　）0，1）中随机地取出两个数所对应的平面区域的面积，及两数之和大于$\frac{5}{6}$对应的平面图形的面积大小，再代入几何概型计算公式，进行解答．

解答 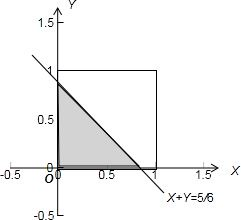解：如图，当两数之和小于$\frac{5}{6}$时，对应点落在阴影上，
∵S_阴影=$\frac{1}{2}•（\frac{5}{6}）^{2}$=$\frac{25}{72}$，
故在区间（0，1）中随机地取出两个数，
则两数之和大于$\frac{5}{6}$的概率P=1-$\frac{25}{72}$=$\frac{47}{72}$．
故答案为：$\frac{47}{72}$．

点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．