
分析 (1)根据对数函数的真数要大于0列不等式组求解定义域.
(2)利用定义证明其单调性.
(3)判断函数的奇偶性,f(a)=4,求解f(-a)的值.
解答 解:(1)函数f(x)=lg(3+x)-lg(3-x)
其定义域满足:$\left\{\begin{array}{l}{3+x>0}\\{3-x>0}\end{array}\right.$,解得:-3<x<3.
故得f(x)的定义域数为{x|-3<x<3}.
(2)由(1)可得f(x)的定义域数为{x|-3<x<3}.设-3<x1<x2<3,
则f(x1)-f(x2)=lg(3+x1)-lg(3-x1)-lg(3+x2)+lg(3-x2)=lg$\frac{(3+{x}_{1})(3-{x}_{2})}{(3+{x}_{2})(3-{x}_{1})}$=lg$\frac{9+3({x}_{1}-{x}_{2})-{{x}_{2}x}_{1}}{9-3({x}_{1}-{x}_{2})-{x}_{1}{x}_{2}}$
因为9+3(x1-x2)-x1x2>9+(x2-x1)-x1x2<0,
∴$\frac{9+3({x}_{1}-{x}_{2})-{{x}_{2}x}_{1}}{9-3({x}_{1}-{x}_{2})-{x}_{1}{x}_{2}}$<1,
即f(x1)-f(x2)<0,所以f(x1)<f(x2),即f(x)是(-3,3)上的增函数;
(3)∵函数的定义域为(-3,3).
∴定义域关于原点对称,
∵f(-x)=lg(3-x)+lg(3+x)=f(x),
∴函数f(x)是偶函数.
∴f(a)=4,则f(-a)=f(a)=4.
点评 本题考查了对数函数的定义域的求法和单调性的判断,奇偶性的运用,具有一定的综合性质,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 |
| y | 5 | 4 | 6 |
| A. | -$\frac{1}{10}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | B. | $\frac{1}{30}$ | C. | 1 | D. | $\frac{7}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大于4 | B. | 小于4 | C. | 等于4 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
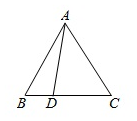 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com