
【题目】如图,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm的内接圆柱. 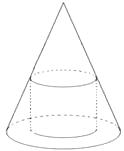
(1)试用x表示圆柱的侧面积;
(2)当x为何值时,圆柱的侧面积最大.
【答案】
(1)解:设所求的圆柱的底面半径为r,它的轴截面如图:
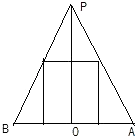
由图得, ![]() ,即
,即 ![]() .
.
∴S圆柱侧= ![]()
(2)解:由(1)知当 ![]() 时,这个二次函数有最大值为6π,
时,这个二次函数有最大值为6π,
∴当圆柱的高为3cm时,它的侧面积最大为6πcm2
【解析】(1)由题意作出几何体的轴截面,根据轴截面和比例关系列出方程,求出圆柱的底面半径,再表示出圆柱的侧面积;(2)由(1)求出的侧面面积的表达式,根据二次函数的性质求出侧面面积的最大值.
【考点精析】根据题目的已知条件,利用二次函数的性质和旋转体(圆柱、圆锥、圆台)的相关知识可以得到问题的答案,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;常见的旋转体有:圆柱、圆锥、圆台、球.
上递减;常见的旋转体有:圆柱、圆锥、圆台、球.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单增函数;若
上的非严格单增函数;若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单减函数.
上的非严格单减函数. ![]() .
.
(1)若函数![]() 为定义在
为定义在![]() 上的非严格单增函数,求实数
上的非严格单增函数,求实数![]() 的取值范围.
的取值范围.
(2)若函数![]() 为定义在
为定义在![]() 上的非严格单减函数,试解不等式
上的非严格单减函数,试解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
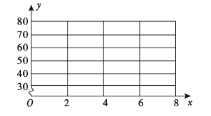
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式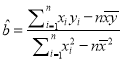 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2 ![]() 和4
和4 ![]() ,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:
| 1 | 2 | 3 | 4 |
| 12 | 28 | 42 | 56 |

(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据:  ,
, ![]() ,
, ![]() .
.
参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体A﹣BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. 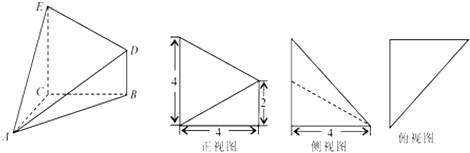
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿海准备购买“海马”牌一辆小汽车,其中购车费用12.8万元,每年的保险费、汽油费约为0.95万元,年维修、保养费第一年是0.1万元,以后逐年递增0.1万元.请你帮阿海计算一下这种汽车使用多少年,它的年平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(k)是满足不等式log2x+log2(52k﹣1﹣x)≥2k(k∈N*)的自然数x的个数.
(1)求f(k)的函数解析式;
(2)Sn=f(1)+2f(2)+…+nf(n),求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com