双曲线x2-y2=1的左焦点为F,点P是双曲线左支上位于x轴上方的任一点,则直线PF的斜率的取值范围是( )
A.(-∞,0]∪[1,+∞)
B.(-∞,0)∪(1,+∞)
C.(-∞,-1)∪[1,+∞)
D.(-∞,-1)∪(0,+∞)
【答案】
分析:根据双曲线方程,得到a
2=1,b
2=1,所以c=
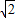
,得左焦点为F(-
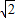
,0).再设点P(x
,y
),可得x
2-y
2=1,且x
<-1,y
>0,根据经过两点的斜率公式,得到PF的斜率关于x
、y
的表达式,化简得:
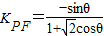
,最后利用换元的方法,结合用导数研究函数的单调性,可得直线PF的斜率的取值范围.
解答:解:设点P(x
,y
),根据点P是双曲线左支上位于x轴上方的点,可得
x
2-y
2=1,且x
<-1,y
>0
双曲线x
2-y
2=1中,a
2=1,b
2=1
∴c=
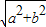
=
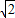
,得左焦点为F(-
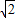
,0)
因此直线PF的斜率为
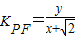
=
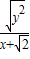
=
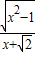
换元:设
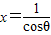
,因为x
<-1,所以θ∈(
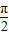
,π)且θ≠
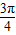
∴
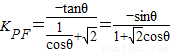
=f(θ)
∵f'(θ)=
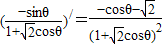
<0恒成立,
∴f(θ)在(
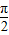
,
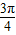
)和(
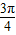
,π)上都是减函数
当θ∈(
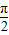
,
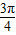
)时,f(θ)<f(
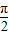
)=-1;
当θ∈(
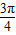
,π)时,f(θ)>f(π)=0
∴K
PF<-1或K
PF>0
故选D
点评:本题借助于双曲线中的一条动直线的斜率取值范围问题,着重考查了双曲线的简单性质和函数的值域与最值等知识点,属于中档题.本题也可以用图象观察的方法得到答案,而题中给出的过程是这个结论的函数理论解释.

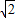 ,得左焦点为F(-
,得左焦点为F(-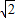 ,0).再设点P(x,y),可得x2-y2=1,且x<-1,y>0,根据经过两点的斜率公式,得到PF的斜率关于x、y的表达式,化简得:
,0).再设点P(x,y),可得x2-y2=1,且x<-1,y>0,根据经过两点的斜率公式,得到PF的斜率关于x、y的表达式,化简得: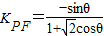 ,最后利用换元的方法,结合用导数研究函数的单调性,可得直线PF的斜率的取值范围.
,最后利用换元的方法,结合用导数研究函数的单调性,可得直线PF的斜率的取值范围.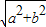 =
=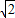 ,得左焦点为F(-
,得左焦点为F(-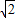 ,0)
,0)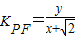 =
=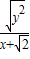 =
=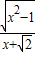
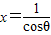 ,因为x<-1,所以θ∈(
,因为x<-1,所以θ∈(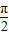 ,π)且θ≠
,π)且θ≠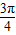
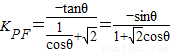 =f(θ)
=f(θ)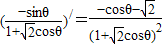 <0恒成立,
<0恒成立,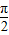 ,
,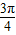 )和(
)和(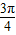 ,π)上都是减函数
,π)上都是减函数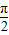 ,
,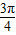 )时,f(θ)<f(
)时,f(θ)<f(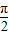 )=-1;
)=-1; 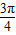 ,π)时,f(θ)>f(π)=0
,π)时,f(θ)>f(π)=0
