
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | -$\frac{1}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{10}{9}$ | D. | $\frac{20}{9}$ |
分析 由ξ的分布列,先求出E(ξ),再求出D(ξ),由此能求出D(η)的值.
解答 解:由ξ的分布列,得:
E(ξ)=-1×$\frac{1}{2}$+0×$\frac{1}{3}$+1×$\frac{1}{6}$=-$\frac{1}{3}$,
D(ξ)=(-1+$\frac{1}{3}$)2×$\frac{1}{2}$+(0+$\frac{1}{3}$)2×$\frac{1}{3}$+(1+$\frac{1}{3}$)2×$\frac{1}{6}$=$\frac{5}{9}$,
∵η=2ξ+2,
∴D(η)=4D(ξ)=4×$\frac{5}{9}$=$\frac{20}{9}$.
故选:D.
点评 本题考查离散型随机变量的方差的求法,是基础题,解题时要认真审题,注意离散型随机变量的分布列和方差性质的合理运用.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
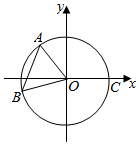 如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.
如图,点A,B是单位圆上的两点,点C是圆与x轴正半轴的交点,若点A的坐标为(-$\frac{3}{5}$,$\frac{4}{5}$),记∠COA=α,且△AOB是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
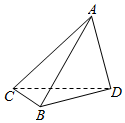 如图,C,D两处相距6000m,∠ACD=45°,∠ADC=75°,∠BDC=15°,∠BCD=30°,AD⊥BD,则点A到B的距离为( )
如图,C,D两处相距6000m,∠ACD=45°,∠ADC=75°,∠BDC=15°,∠BCD=30°,AD⊥BD,则点A到B的距离为( )| A. | 1000$\sqrt{42}$m | B. | 1000$\sqrt{6}$m | C. | 1000$\sqrt{24}$m | D. | 1000m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{36}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com