
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以 下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“ 25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.

附表:
P( | 0.100 | 0 .010 | 0.001 |
k | 2.706 | 6.635 | 10.828 |
![]() ,(其中
,(其中 ![]() )
)
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 ![]() 的列联表,并判断是否有
的列联表,并判断是否有 ![]() 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
【答案】
(1)
解:由已知得,样本中有 周岁以上组工人 名, 周岁以下组工人 名
所以,样本中日平均生产件数不足 件的工人中, 周岁以上组工人有 (人),
记为 , , ; 周岁以下组工人有 (人),记为 ,
从中随机抽取 名工人,所有可能的结果共有 种,他们是: , , , , , , , , ,
其中,至少有名“ 周岁以下组”工人的可能结果共有 种,它们是: , , , , , , .故所求的概率:
(2)
解:由频率分布直方图可知,在抽取的 名工人中,“ 周岁以上组”中的生产能手 (人),“ 周岁以下组”中的生产能手 ![]() (人),据此可得 列联表如下:
(人),据此可得 列联表如下:
生产能手 | 非生产能手 | 合计 | |
周岁以下组 | |||
周岁以上组 | |||
合计 |
所以得:
因为 ,所以没有 的把握认为“生产能手与工人所在的年龄组有关.
【解析】:本题主要考查了,解决问题的关键是(1)样本中日平均生产件数不足 ![]() 件的工人中,
件的工人中, ![]() 周岁以上组工人有3人,
周岁以上组工人有3人, ![]() 周岁以下组工人有2人,从中随机抽取
周岁以下组工人有2人,从中随机抽取 ![]() 名工人,所有可能的结果共有
名工人,所有可能的结果共有 ![]() 种,至少有名“
种,至少有名“ ![]() 周岁以下组”工人的可能结果共有
周岁以下组”工人的可能结果共有 ![]() 种,所求的概率:
种,所求的概率: ![]() (2)在抽取的
(2)在抽取的 ![]() 名工人中,“
名工人中,“ ![]() 周岁以上组”中的生产能手有15人 “
周岁以上组”中的生产能手有15人 “ ![]() 周岁以下组”中的生产能手有15人,列出
周岁以下组”中的生产能手有15人,列出 ![]() 列联表,代入公式求出
列联表,代入公式求出 ![]() 的值,即可判断.
的值,即可判断.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲. 为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
(1)把y表示成x的函数;
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.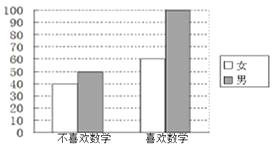
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班学生进行了三次数学测试,第一次有8名学生得满分,第二次有10名学生得满分,第三次有12名学生得满分,已知前两次均为满分的学生有5名,三次测试中至少有一次得满分的学生有15名,若后两次均为满分的学生至少有![]() 名,则
名,则![]() 的值为( )
的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴长为( ) 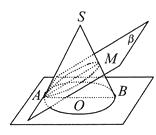
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com