练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知空间四个点A(1,1,1)，B(－4,0,2)，C(－3，－1，0)，D(－1,0,4)，则直线AD与平面ABC所成的角为(　　)

    A．30°         B．45°             C．60°           D．90°


    A

    解析　设平面ABC的一个法向量为n＝(x，y，z)，

    ∵＝(－5，－1,1)，＝(－4，－2，－1)，

    由n·＝0及n·＝0，得

    令z＝1，

    得x＝，y＝－，∴n＝(，－，1)．

    又＝(－2，－1,3)，设AD与平面ABC所成的角为θ，则

    ∴θ＝30°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    右图三角形OAB为用斜二测画法所画的直观图，其原来平面图形的面积是（   ）

    A．4       B．4     C．2    D．8 

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数．

    （I）证明：；

    （II）求不等式：的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的图像大致为 ( )

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证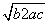<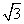a”索的因应是(　　)

    A．a－b>0     B．a－c>0     C．(a－b)(a－c)>0     D．(a－b)(a－c)<0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝(2，－1,1)，b＝(－1,4，－2)，c＝(11,5，λ)．若向量a，b，c共面，则λ＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列{an}的前n项和为Sn，且方程x2－anx－an＝0有一根为Sn－1(n∈N*)．

    (1)求a1，a2；

    (2)猜想数列{Sn}的通项公式，并给出证明．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    解关于的不等式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知抛物线的焦点与双曲线的一焦点重合，则该双曲线的

    离心率为（    ）

    A．    B．     C．      D．

    查看答案和解析>>

    同步练习册答案