
分析 (1)配方即可求出该二次函数在闭区间[0,3]上的最大、最小值,从而得出该函数的值域;
(2)可讨论x2-x=0,和x2-x≠0两种情况,而x2-x≠0时,原函数变成$y=\frac{1}{1+\frac{1}{{x}^{2}-x}}$,而配方可求出x2-x的范围,进而求出$\frac{1}{{x}^{2}-x}$的范围,最后便可得出y的范围,即该函数的值域;
(3)换底公式可将原函数变成$y=lo{g}_{3}x+\frac{1}{lo{g}_{3}x}-1$,而由基本不等式即可求出$lo{g}_{3}x+\frac{1}{lo{g}_{3}x}$的范围,进而即可求出y的范围,即得出该函数的值域.
解答 解:(1)y=x2+2x=(x+1)2-1;
∵x∈[0,3];
∴x=0时,y取最小值0,x=3时,取最大值15;
∴该函数的值域为[0,15];
(2)①若x2-x=0,则y=0;
②若x2-x≠0,$y=\frac{{x}^{2}-x}{{x}^{2}-x+1}=\frac{1}{1+\frac{1}{{x}^{2}-x}}$=$\frac{1}{1+\frac{1}{(x-\frac{1}{2})^{2}-\frac{1}{4}}}$;
∵$-\frac{1}{4}≤(x-\frac{1}{2})^{2}-\frac{1}{4}<0$,或$(x-\frac{1}{2})^{2}-\frac{1}{4}>0$;
∴$\frac{1}{(x-\frac{1}{2})^{2}-\frac{1}{4}}≤-4$,或$\frac{1}{(x-\frac{1}{2})^{2}-\frac{1}{4}}>0$;
∴$-\frac{1}{3}≤\frac{1}{1+\frac{1}{(x-\frac{1}{2})^{2}-\frac{1}{4}}}<0$,或$0<\frac{1}{1+\frac{1}{(x-\frac{1}{2})^{2}-\frac{1}{4}}}<1$;
∴$-\frac{1}{3}≤y<0$,或0<y<1;
∴综上得,该函数的值域为$[-\frac{1}{3},1)$;
(3)y=log3x+logx3-1=$lo{g}_{3}x+\frac{1}{lo{g}_{3}x}-1$;
①若log3x>0,则$lo{g}_{3}x+\frac{1}{lo{g}_{3}x}≥2$,当log3x=1,即x=3时取等号;
∴y≥1;
②若log3x<0,则$lo{g}_{3}x+\frac{1}{lo{g}_{3}x}=-[(-lo{g}_{3}x)+\frac{1}{-lo{g}_{3}x}]$≤-2,当log3x=-1,即x=$\frac{1}{3}$时取等号;
∴y≤-3;
∴综上得,该函数的值域为(-∞,-3]∪[1,+∞).
点评 考查配方求二次函数值域的方法,根据不等式的性质求函数值域的方法,以及基本不等式在求函数值域中的应用,对数的换底公式,应用基本不等式时注意所具备的条件,以及判断等号是否取到.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
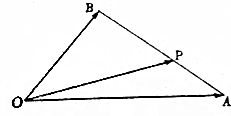 如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.
如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com