
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出⊙C圆心C(4,2),半径r=3$\sqrt{2}$,再求出圆心C(4,2)到直线l:x-y+2=0的距离d=2$\sqrt{2}$,由此能求出结果.
解答 解:⊙C:(x-4)2+(y-2)2=18的圆心C(4,2),半径r=$\sqrt{18}$=3$\sqrt{2}$,
圆心C(4,2)到直线l:x-y+2=0的距离d=$\frac{|4-2+2|}{\sqrt{1+1}}$=2$\sqrt{2}$,
∴⊙C:(x-4)2+(y-2)2=18上到直线l:x-y+2=0的距离为$\sqrt{2}$的点有3个.
故选:C.
点评 本题考查满足条件的点的个数的求法,是中档题,解题时要认真审题,注意圆的性质及点到直线的距离公式的合理运用.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
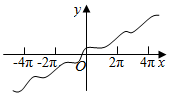
| A. | f(x)=x+sinx | B. | f(x)=$\frac{cosx}{x}$ | C. | f(x)=xcosx | D. | f(x)=x(x-π)(x-3π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示:
某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com